Chap. 20 Decision Analysis
20.1 前言
決策理論為那些可用來在不確定下協助管理者制定決策的機率性OR工具之一。模式組成包括：
1 決策者的有限個行動方針 (action)
2 所面對的nature的可能變化情況
3 每個行動- nature情況的組合所引起的損失 (loss)
目標在選擇可極小化損失的行動。
例：決策表 (損失表 Loss Table)
|
|
Nature 狀況 |
大中取小 |
|
|
行動 |
下雨 |
不下雨 |
|
|
帶雨具 |
0 |
3 |
3 |
|
不帶雨具 |
6 |
0 |
6 |
例：某石油公司擁有的土地，據說地下蘊藏石油。該公司將此些土地依其可能蘊藏的石油量以桶數計算，分成四類：50萬、20萬、5萬桶油井與枯油井。如今該公司需決定是否鑽探、或將以無條件出租，或以有條件出租，而依開採量計算租金。鑽井成本如下：產油井10萬、枯油井7.5萬。每桶油的淨利為1.5 US$，無條件租約的租金可得4.5萬，有條件租約的規定則是若可採得20或50萬桶，則每採一桶該公司可得0.5 US$，否則毫無所得。
Table 20.1 石油公司利潤表
|
|
50萬桶油井 |
20萬桶油井 |
5萬桶油井 |
枯油井 |
|
自行開採 |
65萬 |
20萬 |
-2.5萬 |
-7.5萬 |
|
無條件出租 |
4.5萬 |
4.5萬 |
4.5萬 |
4.5萬 |
|
有條件出租 |
25萬 |
10萬 |
0 |
0 |
Loss Table
|
|
50萬桶油井 |
20萬桶油井 |
5萬桶油井 |
枯油井 |
大中取小 |
|
自行開採 |
-65萬 |
-20萬 |
2.5萬 |
7.5萬 |
7.5 |
|
無條件出租 |
-4.5萬 |
-4.5萬 |
-4.5萬 |
-4.5萬 |
-4.5 |
|
有條件出租 |
-25萬 |
-10萬 |
0 |
0 |
0 |
大中取小策略是極度保守的準則，用此原則是假設對手是有意識的，其將盡其所能來贏取勝利。一般而言，自然狀態並非惡意的對手，決策者並非一定要防範此等事情發生而採最保守的策略。
在博奕理論中所涉及的Payoff Table中所列為博奕者甲贏乙的數字，此處的損失表中的數字所代表是博奕者甲輸給乙
(Nature)的數字，兩者意義正好相反。
在決策分析中並不是不能用與博奕理論中所使用Payoff Table，只是此時需改用小中取大原則。
20.2a缺乏nature 狀況的資料時
必須依據nature 狀況的相關資料，才能找出能維持損失於最小的最佳行動。在缺乏nature 狀況的相關資料時較保守的做法是採：
大中取小決策過程：(minimax loss criteria)
最大可能策略：maximum likelihood criteria，先針對nature
狀況的各個可行性做「事前(prior)的機率分配」，再選取最大可能欄中之最小值。
無須資料的貝氏(Bayes)決策過程：Bayes' decision rule，先針對nature 狀況的各個可行性做「事前(prior)的機率分配」，再由各期望值中找最小者。
如下表所示，大中取小策略選出活動2，最大可能策略選出活動4，貝氏策略選出活動4。
|
|
Nature 狀況 |
大中取小 |
最大可能 |
Bayes |
||
|
|
N1 |
N2 |
N3 |
|
Prob. of N1=1/2, N2=1/3, N3=1/6 |
|
|
A1 |
4 |
7 |
3 |
7 |
4 |
29/6 |
|
A2 |
5 |
2 |
4 |
5 |
5 |
23/6 |
|
A3 |
8 |
6 |
10 |
10 |
8 |
46/6 |
|
A4 |
3 |
1 |
9 |
9 |
3 |
20/6 |
|
|
|
|
|
Min=5 |
Min=3 |
Min=20/6 |
若表中數值為Payoff value 則改採小中取大策略(maximin payoff criteria)，最大可能策略改選取最大可能欄中最大值，貝氏策略改選取期望值中之最大者。貝氏策略使用了所有資訊，若所有資訊的可信度高，則此應為最好的方法。
不同的「事前(prior)的機率分配」，也會產生不同的決策，如下例說明：
某廠商想決定在滑雪季節對滑雪設備的庫存量，天候狀況可分為適於滑雪、普通與不適合三類，相關機率為0.5, 0.4 與0.1或0.1, 0.4 與0.5。決策表如下：
|
|
Nature 狀況 |
Bayes |
Bayes |
||
|
|
N1 |
N2 |
N3 |
N1=0.5, N2=0.4 ,N3=0.1 |
N1=0.1, N2=0.4 ,N3=0.5 |
|
A1 |
-20 |
-12 |
-6 |
-15.4 |
-9.8 |
|
A2 |
-16 |
-16 |
-8 |
-15.2 |
-12 |
|
A3 |
-12 |
-12 |
-12 |
-12 |
-12 |
例：在鑽油例中，假設各項之事前機率與在各自然狀況下選擇各行動(a)的相對損失值如下表：
|
|
50萬桶油井 0.1 |
20萬桶油井 0.15 |
5萬桶油井 0.25 |
枯油井 0.5 |
Bayes |
|
a1自行開採 |
-65萬 |
-20萬 |
2.5萬 |
7.5萬 |
L(a1)= -5.125萬 |
|
a2無條件出租 |
-4.5萬 |
-4.5萬 |
-4.5萬 |
-4.5萬 |
L(a2)= -4.5萬 |
|
a3有條件出租 |
-25萬 |
-10萬 |
0 |
0 |
L(a3)= -4萬 |
貝氏策略為利用事前機率做決策支援的方法。依據貝氏策略，決策者應選擇能使期望損失值為最小的行動，期望損失L(a)可由以可能自然狀態為定義域之事前分配機率算出，L(a)稱為損失函數(Loss Function)。
即 L(a)=E[L(a, 
)]= 
, if 
為離散。若為連續則以積分取代Sum 符號。
L(a1)=
E[(L(a1, 
)]=-65*(0.1)-20*0.15+2.5*0.25+7.5*0.5 = -5.125
L(a2)= E[(L(a2, 
)]=-4.5*(0.1)-4.5*0.15-4.5*0.25-4.5*0.5 = -4.5
L(a3)= E[(L(a3, 
))=-25*(0.1)-10*0.15+0*0.25+0*0.5 = -4
決策將改為自行開採，且期望的損失為-5.125萬=利潤為5.125萬US$。
20.2b 缺乏nature 狀況的相關資料時的其他法則 (補充)
Laplace Criteria
One select the action ai yielding the largest expected gain or minimum expected loss. That is, select the action ai* corresponding to：
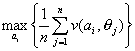, if v is the payoff matrix
where,
1/n is the probability that 
(j=1,2,…,n) occurs.
Savage Minimax Regret Criteria
由損失表中各欄之值扣除該欄的最小值可得悔惜表，採用大中取小決策過程，配合損失表或悔惜表可能得出不同結果，如下表黃區所示：
|
損失表 |
|
悔惜表 |
||||||||
|
|
N1 |
N2 |
N3 |
Max |
|
|
N1 |
N2 |
N3 |
Max |
|
A1 |
3 |
8 |
1 |
8 |
|
A1 |
0 |
4 |
0 |
4 |
|
A2 |
9 |
6 |
5 |
9 |
|
A2 |
6 |
2 |
4 |
6 |
|
A3 |
7 |
4 |
8 |
8 |
|
A3 |
4 |
0 |
7 |
7 |
|
A4 |
5 |
5 |
6 |
6 |
|
A4 |
2 |
1 |
5 |
5 |
此種策略適用於如同以下的情況：
|
|
N1 |
N2 |
Max |
|
N1 |
N2 |
Max |
|
A1 |
11000 |
90 |
11000 |
|
1000 |
0 |
1000 |
|
A2 |
10000 |
10000 |
10000 |
|
0 |
9910 |
9910 |
依照悔惜表選出的行動比依照損失表選出者要好多了。
循上例：
|
|
Nature
狀況 |
Laplace |
Savage
Minimax |
||||||||
|
|
N1 |
N2 |
N3 |
|
N1 |
N2 |
N3 |
|
|||
|
A1 |
4 |
7 |
3 |
14/3 |
1 |
6 |
0 |
6 |
|||
|
A2 |
5 |
2 |
4 |
11/3 |
2 |
1 |
1 |
2 |
|||
|
A3 |
8 |
6 |
10 |
24/3 |
5 |
5 |
7 |
7 |
|||
|
A4 |
3 |
1 |
9 |
13/3 |
0 |
0 |
6 |
6 |
|||
|
|
|
|
|
Min=11/3 |
|
|
|
Min=2 |
|||
Hurwica Criteria
對Loss
Table 而言，this criteria selects the
action that yields
此法允許在兩極限值中取加權平均。當
此法即為 minimax 大中取小法則。
|
|
Nature
狀況 |
Hurwica
Criteria |
|||||
|
|
N1 |
N2 |
N3 |
Min |
Max |
|
|
|
A1 |
4 |
7 |
3 |
3 |
7 |
5 |
|
|
A2 |
5 |
2 |
4 |
2 |
5 |
3.5 |
|
|
A3 |
8 |
6 |
10 |
6 |
10 |
8 |
|
|
A4 |
3 |
1 |
9 |
1 |
9 |
5 |
|
20.3 具有nature 狀況的資料時的Bayes 決策過程
在鑽油例中，假設可以$12000之代價取得進一步地質探勘資料，探測結果分為四類：1. 該地有封閉性結構，2. 可能有封閉性結構，3. 有非封閉性結構，4. 無任何結構。依過去100例的鑽井經驗中可得下表：
表22.3
|
探測類別 |
50萬桶油井 |
20萬桶油井 |
5萬桶油井 |
枯油井 |
|
1 |
7 (7/12) |
9 (9/16) |
11 (11/24) |
9 (9/48) |
|
2 |
4 (4/12) |
3 (3/16) |
6 (6/24) |
13 (13/48) |
|
3 |
1 (1/12) |
2 (2/16) |
3 (3/24) |
15 (15/48) |
|
4 |
0 (0/12) |
2 (2/16) |
4 (4/24) |
11 (11/48) |
|
Sum |
12 |
16 |
24 |
48 |
20.3.1 風險函數 (Risk Function)
定義為R(d,
) =E[L(d[X],
)]，
進一步決策d1[X]：探測結果(X)為類別1則採行動a1，類別2或3則採行動a3，類別4則採行動a2。
R(d1,
) =-650000(7/12)-45000(0)-250000(4/12+1/12)+12000 = -471333
R(d1,
) =-200000(9/16)-45000(2/16)-100000(3/16+2/16)+12000 =
-137375
R(d1,
) =25000(11/24)-45000(4/24)+0(6/24+3/24)+12000 = 15958
R(d1,
) =75000(9/48)-45000(11/48)+0(13/48+15/48)+12000 = 15750
如上所示，給定一新的策略d[X]可求出新的風險函數R(d,
)。風險函數可作為界定最優性的一種方法，最優決策函數可定義為在每一
值之下，風險皆為最小的決策函數。然而，此最優決策函數並非恆存在。
20.3.2 貝氏風險
貝氏程序提供一個較佳的方法：貝氏風險 (Bayes’ risk , B(d) )作為界定最優性的另一種方法。
B(d)=
有此定義，即可應用貝氏原則來選擇使B(d)最小的函數d為最終決策。即以新資料將「事前的(Prior)機率分配」更新(update)為「事後的(posterior)機率分配」。
假設以下資料均已知：
想要決定
(在TextBook 中以
表示)
鑽井例：
|
|
|
|
|
|
Sum |
|
x=1 |
0.166 |
0.24 |
0.327 |
0.267 |
1 |
|
x=2 |
0.129 |
0.108 |
0.241 |
0.522 |
1 |
|
x=3 |
0.039 |
0.087 |
0.146 |
0.728 |
1 |
|
x=4 |
0 |
0.107 |
0.238 |
0.655 |
1 |
假設探測結果得知該地為類別(3)，表示有非封閉性結構。只需求上表中x=3該列的事後分配機率，再計算每一行動ai的期望損失Lh(ai)。
|
Lh(a1) = E[L(a1, |
= -650000(0.039)-200000(0.087)+25000(0.146)+75000(0.728)+12000 |
=27500 |
|
Lh(a2) = E[L(a2, |
= -45000 + 12000 |
=-33000 |
|
Lh(a3) = E[L(a3, |
=-250000(0.039)-100000(0.087)+12000 |
=-6450 |
)]
)]
)]
依照貝氏程序選擇行動2，即該公司無條件出租土地。由以上可知，由於增加了探測資料改變了決策者的行動。
20.3.3 事後分配機率的計算
事前分配機率以
為隨機變數，
之邊際分配即為
之事前分配機率值
，新增資料以X為隨機變數，假設係依據
=k的Poisson 機率分布，則X之條件機率分配函數可用
表示，
與X的聯合機率分配可用
表示。
X之邊際分配
亦可求得，如下式所示：
最後，給定X=j時之
的條件分配，即為給定X=j時之
的事後分配，令j之值以x表示，則
。
鑽油井例：
事前機率
假設探測結果得知該地屬於X=3類別，即需求出
, k = 1,2,3,4.
為該油井產量為編號k之類別，探測結果為類別3之機率，此機率可直接由下表查得：
|
|
50萬桶油井 |
20萬桶油井 |
5萬桶油井 |
枯油井 |
|
事前機率 |
0.1 |
0.15 |
0.25 |
0.5 |
|
探測類別1 |
7/12 |
9/16 |
11/24 |
9/48 |
|
探測類別2 |
4/12 |
3/16 |
6/24 |
13/48 |
|
探測類別3 |
1/12 |
2/16 |
3/24 |
15/48 |
|
探測類別4 |
0/12 |
2/16 |
4/24 |
11/48 |
(1/12)(0.1)+(2/16)(0.15)+(3/24)(0.25+(15/48)(0.5)=0.2147
，
，
彙整：表20.5
|
事前分配 |
0.1 |
0.15 |
0.25 |
0.5 |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
探測類別 |
|
|
|
|
|
|
|
|
SUM=C |
探測類別 |
|
|
|
|
|
x=1 |
7/12 |
9/16 |
11/24 |
9/48 |
0.0583 |
0.0844 |
0.1146 |
0.0938 |
0.3511 |
1 |
0.166 |
0.24 |
0.327 |
0.267 |
|
x=2 |
4/12 |
3/16 |
6/24 |
13/48 |
0.0333 |
0.0281 |
0.0625 |
0.1354 |
0.2593 |
2 |
0.129 |
0.108 |
0.241 |
0.522 |
|
x=3 |
1/12 |
2/16 |
3/24 |
15/48 |
0.0083 |
0.0188 |
0.0313 |
0.1563 |
0.2147 |
3 |
0.039 |
0.087 |
0.146 |
0.728 |
|
x=4 |
0/12 |
2/16 |
4/24 |
11/48 |
0.0 |
0.0188 |
0.0417 |
0.1146 |
0.1751 |
4 |
0.0 |
0.107 |
0.238 |
0.655 |
另例：
假設依據過去的資料已知一特定季節之滑雪裝備的需求量是一變異數為10，與依據整季中滑雪情形而定的平均數為5,10或15單位的常態分配。令
X = 一特定季節之滑雪裝備的需求量
|
|
|
|
|
|
|
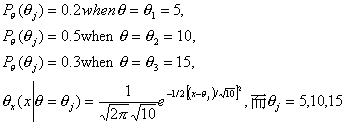
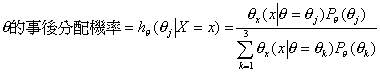
A1庫存量：大 |
-8 |
-12 |
-20 |
-13.6 |
|
A2庫存量：中 |
-10 |
-14 |
-14 |
-13.2 |
|
A3庫存量：小 |
-12 |
-12 |
-12 |
-12 |
|
|
|
|
|
|
|
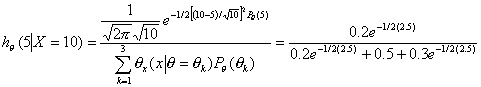
A1庫存量：大 |
-8 |
-12 |
-20 |
-12.716 |
|
A2庫存量：中 |
-10 |
-14 |
-14 |
-13.644 |
|
A3庫存量：小 |
-12 |
-12 |
-12 |
-12 |
由於增加了X=10 的資訊，A之決策由大庫存量改為中庫存量且利潤由13.6單位增加至13.644單位。
常態分配的連續隨機變數的機率值為
其中，x的期望值或平均數為
，變異數為
。
20.3.4 資料之價值
有、無資料時以貝氏策略分析所得期望值的差，即為該資料的價值。
20.4 決策樹
決策樹由分歧點(forks)和分枝(branches)構成，決策分歧點用方塊表示，機遇分歧點用圓圈表示，分枝為由分歧點發出的直線。當決策者面臨決策分歧點時，應採行其中一分枝；當面臨機遇分歧點時則由機遇事件決定應選哪一分枝。
所需之計算與前面所述相同，包括邊際機率、事後機率與貝氏風險值等。可循之每一路線的損失皆於終點註明。
圖20.1, 圖20.2
20.5 效用尺度 (Utility Scale)
Case 1. 獨得10000 或 0 的機率各半
Case 2. 穩贏 4000.
儘管依期望值計算Case 1 優於 Case 2，但多數人願意選擇 Case 2。決策者的賭性 (個人偏好)需定義另一個效用尺度來表示。
20.6 演藝團之例
|
演出日為 |
雨天 |
陰天 |
晴天 |
|
有演出 |
損失15000 |
5000 |
-10000 |
|
無演出 |
損失1000 |
1000 |
1000 |
演出前臨時取消需罰款1000元，氣象局預測演出日為雨天、陰天或晴天的機率分別為0.1, 0.3, 0.6。取得氣象資料的成本為1000元。氣象局在過去的預測成果如下表：
|
|
實際為雨天 |
實際為陰天 |
實際為晴天 |
|
預測為雨天 |
0.7 |
0.2 |
0.1 |
|
預測為陰天 |
0.2 |
0.6 |
0.2 |
|
預測為晴天 |
0.1 |
0.2 |
0.7 |
邊際機率
|
|
實際為雨天 |
實際為陰天 |
實際為晴天 |
SUM |
|
預測為雨天 |
0.07 |
0.06 |
0.06 |
0.19 |
|
預測為陰天 |
0.02 |
0.18 |
0.12 |
0.32 |
|
預測為晴天 |
0.01 |
0.06 |
0.42 |
0.49 |
事後機率
|
|
實際為雨天 |
實際為陰天 |
實際為晴天 |
|
預測為雨天 |
0.07/0.19=0.368 |
0.06/0.19=0.316 |
0.06/0.19=0.316 |
|
預測為陰天 |
0.02/0.32=0.062 |
0.18/0.32=0.563 |
0.12/0.32=0.375 |
|
預測為晴天 |
0.01/0.49=0.02 |
0.06/0.49=0.122 |
0.42/0.49=0.857 |
參見下圖
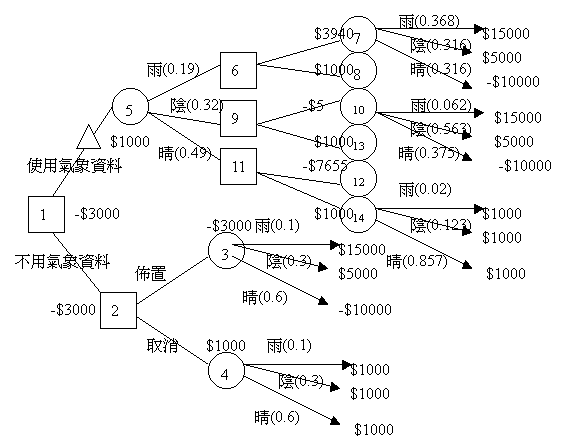
氣象情報之價值：
使用或不使用氣象情報之最終期望損失分別為-3563與-3000，由此可知氣象情報之價值不應高於此差額563元。
完全正確的氣象情報的價值：
完全正確的氣象情報的期望損失為(雨天與陰天都取消，晴天才演出) 1000*0.1+1000*0.1 –10000*0.6=-5600，
不使用氣象情報之期望損失為 –3000，完全正確的氣象情報的價值不應高於此差額2600元。
