MATLAB������
�@
�x�j�ͪ����q�t ���B��б�
�ѡB�p��ާ@
MATLAB���
�p�e�ҭz�AMATLAB�ҳB�z����ƫ��A��ڤW�Ȧ��@�ءA�Y������x�}�A���M�x�}�����U�p���i�ର��������ƫ����C�Ҧ����ܼƧ��H�x�}�����A�X�{�A�Eť�_�ӹ�b���i��ij�A���L�o�]�O MATLAB���ҥH����MATLAB�A�������I�]�N�b�o�̡C�b�Y�DZ��p�A�@�ӱ`�ƧY�i�����@�Ӣ��A�����x�}�A���M�A���o�˻{���]�L�ҿסA���O�`�ƴN�����O�`�ơA�ӦV�q�h������x�}�ΦC�x�}�C
�bMATLAB���A��x�}�P�C�x�}�ȬO�@��x�}���S���Ҥl�Ӥw�A�@��x�}�����P���B�z�覡�G
- �H�@�t�C�椸��J�C
- �Q�ιw�]����Ʋ��͡C
- �b���ɮפ����͡C
- �ѥ~������ɤ�������J�C.
MATLAB�O�N�@���ƥH�x�}�ΦV�q���A�ާ@�C�G�@�ӯx�}��i�����b���O�椧>>�U��J�A�Ҧp�G
�@
>>A = [1 2 3; 4 5 6; 7 8 9];
�ϬO�@�Ӣ��A�����x�}�A�Ĥ@�檺�������T���A�U�����H�ܤ֤@�ӪŮ���j�F��P�涡�h�H";"���j�C�ȱo�`�N���O���O��̫������� ";"�O�㦳�S�O�N�q�A��������ޡC��ڤWMATLAB�b���h�O���ܳo����O�����浲�G���b�ù��W��ܡA�]���A�ݤ��쥦���B��G�A���x�}�ȫh�O�b�ϸ̡A�b�q�����C�q�`�g���O�ɮɡA�b���O��᧡�[�W�o�Ӥ����A�H�קK�W��ܥX�\�h���ݭn���F��C���O���ɬ��������ت��A�i�N������h���A�H�[�ݨ��ڤ��B��G�C���M�W�z��J��������A�Y�Q���D�x�}�Ϥ����e�ɡA�h������J>>A�Y�i�A�ù�����ܱN�p�U�G
�@
1
2 3
3 4
5
6 7
8
�t�@�ؿ�J�i�H���[�����A���O�j������A��i�F��ۦP���ĪG�G
>> B = [ 1 2 3 4
�@�@5 6 7 8
�@�@9 10 11 12]
B =
1 2 3 4
5 6 7 8
9 10 11 12
���F�x�}����A�Y�i�i��U���ާ@�A�䤤�̱`�����O�N�x�}���m�G�Y�b�@�x�}��[�@�J, �p:
>> C = B'
C =
1 5 9
2 6 10
3 7 11
4 8 12
�ȱo�`�N���O�A�o�@�J���N?���ƼƦӨ��h�����P�����A���O�N���ӽƼƤ��@�m�ƼƤ��N�C�G�Y�����m�A���אּ .',��Y�b�@�J���e�n�[�@�I.���D�Ƽƫ����x�},����Ӿާ@�Ÿ����\��h�ۦP�C
�Y�n���ͤ@�Ӧ�V�q����ơA�h�i��J�p�U�G
�@
>>V = [1; 2; 3];
�h���J���A MATLAB �|�^���p�U�G:
�@
1
2
3
�Ӧ�V�q�h�i��J�p�U�G
�@
>>V = [1 2 3 4];
���J���A�Y�|��ܡG
�@
1 2 3 4
�C�V�q��i�Ѧ�V�q�H�˸m�k���͡A�Ҧp�G�e�大 V�V�q�Y�H�˸m�ާ@���覡�p V'�A�αN��˸m��m��t�@�ܼƢ㤤�A�p�G
�@
>>V=[1
2 3 4]; % row vector
>>U=V';
% column vector
>>U
1
2
3
4
���B�X�{�� "%"���ܥH�ᤧ��r�������A���|�Q����C
�Y�n���ͤ@�ӦC�V�q���ܼơA��ȥѶ��Z��1���A��d��0��10���A�h�Q��MATLAB��²��A�u�n����U�������O�G
�@
>>[t]
= 0:1:10;
>> t=0:0.1:10
t =
Columns 1 through 7
0
0.1000 0.2000
0.3000 0.4000
0.5000 0.6000
Columns 8 through 14
0.7000
0.8000 0.9000
1.0000 1.1000
1.2000 1.3000
�K �K
Columns 92 through 98
9.1000
9.2000 9.3000
9.4000 9.5000
9.6000 9.7000
Columns 99 through 101
9.8000
9.9000 10.0000
�W�����N��ۦP�A�e�̸��V���At ��[]�A�_�Ӫ��ܨ䬰�x�}�A������[]�]�S���Y�C�u�O�᭱�]���S��������;���At �����e�|�b���f����ܥX�ӡC���ᰣ�D�A�A�Nt�����e�Υt�~�覡���ܡA�_�h���O�@�ӦC�x�}�C�A�]�i�H��t�o�@�ӦV�q�ܼƧ@���t�@�Ө�Ƥ���X�J�ѼơC�Ҧp�G
>>
x=sin(t)
x =
Columns 1 through 7
0
0.0998 0.1987
0.2955 0.3894
0.4794 0.5646
Columns 8 through 14
0.6442
0.7174 0.7833
0.8415 0.8912
0.9320 0.9636
�K �K
Columns 92 through 98
0.3191
0.2229 0.1245
0.0248 -0.0752 -0.1743 -0.2718
Columns 99 through 101
-0.3665
-0.4575 -0.5440
�h�A�x�}�ұo���ƭ���������sin��ơA�ӣA�笰�C�x�}�A�j�p�P
t �ۦP�C
�g�L�o�f�ѻ���A�ڭ̷Q�Q��MATLAB�̱j�O���ϥܪk�Ӫ��ܨ䵲�G�A�h�i�N�W�z�o�줧[x]�x�}�ȻP�ɶ� [t]��������Yø�s�@�ϡA�o�ӫ��O���e�H��t�~���`�A�͡A���i�H������p�U�G �]�`�N�G�᭱�� 'r' �ѼƥN���ά���u���N��^
�@
>>plot(t,x,'r')
���G�G
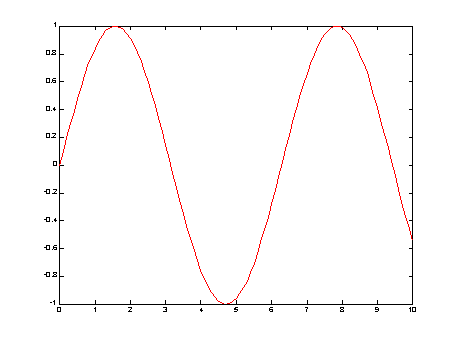
�� 1. y=sin(x)
�A�@�A�h��²��A�H���n�b�{���]�p�Wø�X�o�˪��ϡA�n��@�ӤW�Ȫ��\�ҡA�{�b�i�O�b�@�ӫ��O�U�����A�u�O�ŷ��F�C�{�b�A�A�i�H�Ϋ������\�ұN���h��A���w���a��h�A�^�b���i���tģ�@�f�C���O�i�O���A�o�~�}�l�Ӥw�O�C�`�N�Ϣ������y�Ч����[�ХܡA�Ϫ��W�٤]���R�W�C�o�Ӧp��O�n�H�����o�@�`�ڭ̦b�᭱���`����Q�סA�p�G�A�����Ϊ��ܡA�]�i�H��help plot���ݬݥ����Ϊk�ΰѦҨ��U�A���C�ܤ֧A�i�H�Pı�� MATLAB �O�@�ӱj�Ӧ��O���u��A���A�i�H��|������Ω�\�h���P���h���C�Q�� MATLAB�A�A���i�H���[��Y�@�w�]����Ʃο�J��Ƥ��ܤơC
�W���ұo�줧��ӯx�}[x]�P[t]����101�����C�x�}�A��j�p�H1x101���ܡC�ѼƾǤW�o���A��ӯx�}�ۭ��A�����O�b�j�p�۰t�X�A�_�h�|�X�t���C�Ҧp�A�N�e���ҩw�q����ӯx�}�ۭ��|�����G�G
>>
A=x*t
??? Error using ==> *
Inner matrix dimensions must agree.
�o���ܨƦ����ߡA�ӿ��b���̩O�H�ӯx�}�����k��Ĥ@�ӯx�}x����ƻP�ĤG�x�}t���C�����ۦP�~��ۭ��A�Y[1x101]*[101x1]��[101x1]*[1x101]�C�H�e�̬��ҡA�h�ĤG�x�}[t]�������ର��x�}[101x1]�A�Ө䵲�GA����[1x1]�x�}�C�p��N[t]�����ର��x�}�O�H��²��A�u�n�bt�᭱�[�W�����A�Ρ@t���@�ڭ̺٬����m�A���ڭ̥��ݬݡG
>>
t'
ans =
0
0.1000
0.2000
�K
9.8000
9.9000
10.0000
�G�@t���@��M�w������x�}�A��j�p��101x1�C���@�ӫ��O�i���D����x�}���j�p�A�s��size()�A�ڭ̥i�H�ոլݡG
>>size(t')
ans =
101
1
�b�W�����Ҥl���A�ڭ̵o�{��i�����b���O���U���J�@�ӭp�⪺���z���O�A�䵲�G�o��b�@���ܼƥsans�̡C���M�A�p�G�A�Ʊ�N���G��b��L�ܼƤ��A�S���D�I�u�n�N���ܼƦW�ٸm��������Y�i�C�Ҧp�Gmyans=
size(t'); �hmyans�Y�|�s�����ܪ�����(���O�Amyans�o���ܼƪ�size�S�O�p��O�H)�C�b�o�̥� t �x�}�ର t'�A�ڭ̺٥������m(Transpose)�C
�g�L�e�������ˤ���A�ڭ̦^��x�}���k�����D�C�{�b�w�� x*t�� ���ӲŦX�����{�ǤF�A���O�ܡH�ڭ̨Ӱ����ݡG
>>
A=x*t��
A =
75.6724
>>size(A)
ans =
1
1
�n���S�����~�A�o�N��F�C��MA���j�p��1x1�A��Ȭ�75.6724�C�H�q�����ܡA�G�x�}�ۭ��A��j�p����[m x n] x [n x p]=[m x p]�A�k�䤧���G�Y���x�}�ۭ��ᤧ�j�p�C�ƹ�W�o�������W�h�b�u�Ƹ̦��N���o�ܦh�A�o�̥u�O�A�@���j�աA���I�e�D�K���A�L�צp��u�O�@�y�ܡA������MATLAB�٬O�A�q�ƾǪ��k�h�Ӥw�C
�x�}�ۭ��A�٦��\�h���쪺�Ҥl�C�J�M�j�p�n�۲ŦX�A����Ӥj�p�ۦP����x�}���ۭ��h�O�@�L�U�ҤF�A�ƹ�W�]�O�p���A�B�ݤU�ҡF
�@
?A=[1 2 3;4 5 6;7 8 9]�@�@�H�إߤ@�Ӣ��梲�x�}��
A =
1 2 3
4 5 6
7 8 9
?A*A
ans =
30 36 42
66 81 96
102 126 150
?A*A*A
ans =
468 576 684
1062 1305 1548
1656 2034 2412
?A^3
ans =
468 576 684
1062 1305 1548
1656 2034 2412�@�@�H���G�PA*A*A�ۦP!
���G�n�����ܥ��`�A��M�Y�ϯx�}���T����A�]�������N�q�C���O�Y�@��.^�ɡA�䵲�G�N�������ˤF�A���O�ܡH
�@
?A.^3
ans =
1 �@ 8 �@27
64 125 216
343 512 729
�@
�W���o�Ӱ��D�b���̩O�H���Ǯɭԧڭ̨ä��O�u���n���o��[�ۭ�]���ơA�]�����˪����G�ӹL���g�F�A���ɧڭ̶ȬO�Ʊ��x�}�����۹��������ش����r���A�M�ᵲ�G���M�O��Ӥ��x�}�j�p�A�Ϊ̬O��Ӫ��x�}�A�ȱN�x�}�������بҦp�ۦ業��ζ}��A�p���Ӥw�C�����AMATLAB�۳Ф@�Ӿާ@���A�Y�b�ާ@���e���[�r�I��.���A�u�n�N�o�r�I�m��ާ@�����e���A�Y���ܴN�O�o�ؤ@��@���B�z�覡�A�e�������G���Y�O�U�����T����C�U�C�]�O�@�Ӧn�Ҥl�G
�@
E
= [1 2;3 4]
F = [2 3;4 5]
G = E .* F
E =
1 2
3 4
F =
2 3
4 5
G =
2 6
12 20
�@
�@
�Y���H�e��A=x*t���Ϳ��~���ҡA�A���L�ҳo�إΪk�G
>>A=x.*t
A =
Columns 1 through 7
0
0.0100 0.0397
0.0887 0.1558
0.2397 0.3388
Columns 8 through 14
0.4510
0.5739 0.7050
0.8415 0.9803
1.1184 1.2526
�K
Columns 85 through 91
7.1786
6.7871 6.3158
5.7678 5.1473
4.4591 3.7091
Columns 92 through 98
2.9038
2.0506 1.1574
0.2329 -0.7139 -1.6735 -2.6361
Columns 99 through 101
-3.5915
-4.5296 -5.4402
>>size(A)
ans =
1
101
�w��o�@�ӨҤl�A�ڭ̤]�i�H�ΦP�˪�ø�Ϥ�k�A�ݬ�A�� t �ү�i�{���ҧ��R���G
>>plot(t,A,'r')
���G�G
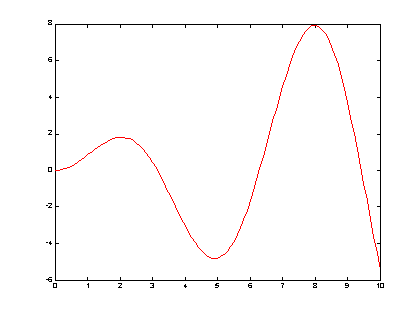
Fig
2. y=
x sin(x)
�@
�@
�P�e�����ƭȦL�Ҥ@�U�A�ݯx�}A�O�_���������ۭ������G�C��A���j�p���M��[1x101]�C�ҥH�b�W�����A�ݭӯS�O�`�N�b*�����e���@���I�A�o�ä��O�����A�ӬO����S�O�N�q�C���������@�I�h�|�դ��d���C
�@
�b���S�O�����@�U�A���ήɭY�J����ƫ������Ʀr�A�Ҧp 2.34e-9, �䶡�������o�d�Ů�A�_�h���|�ݦ��x�}����Ӷ��ءC�n�C�X�j�x�}�ɡA�̦n�ϥ�M-file�A���˷|����e�������CMATLAB �����ب�Ʀprand�Bmagic�Bhilb���A�Ϫ�Ǫ��H�i�H�Q�Υ��i��U���m�ߡC�o�dz��|���ͤ@�� n x n ���x�}�A�H n=3 ���ҡA���O�p�U�G
>>rand(3)
ans =
0.5828
0.3340 0.5798
0.4235
0.4329 0.7604
0.5155
0.2259 0.5298
>>magic(3)
ans =
8
1 6
3
5 7
4
9 2
>>
hilb(3)
ans =
1.0000
0.5000 0.3333
0.5000
0.3333 0.2500
0.3333
0.2500 0.2000
���O rand(n) �P rand(m,n) �N�ӧO���� n�An �P m�An �üƯx�}�C�� magic(n) �h���� n�An �����N����x�} (�Y��P�C���M���ۦP)�F hilb(n) �h���� n�An ���B�S�]Hilbert �^�x�}�A�O�@�ثD�`���}����U���x�}�A��U�����ȥH1/(i+j-1)�p��A�䤤 i �P j ���O���x�}���C�ƻP��ơC�@��x�}��i�H�� for-loop���j����O���͡A�ӫe���ҥΤ� [0:0.1:10] �]�O�`�Ϊ���k�C
�x�}�ΦV�q�x�}�����إi�H�Q�άA���������ƨӪ��ܡC�Ҧp A(2,3) ���ܢϯx�}���ĤG�C�ĤT��B�����ءA�� x(3) �h�N���ĤT�y�Ф��V�q�A�C
�@�ӯx�}���ϸm��i�̤U�z���ާ@�D�o�G
>> X = inv(E)
X =
-2.0000 1.0000
1.5000 -0.5000
��S�x�V�q�ȡ]eigenvalues�^�h���G
>> eig(E)
ans =
-0.3723
5.3723
�@�ӯx�}���h�����S�ʫY�ƥ�i�̤U�k�D�o�A��Y�Ʀ����@�C�V�q�G
�@
>>p
= poly(E)
p =
1.0000 -5.0000 -2.0000
�Ө̤u�{�ƾǤ��[���A�@�h�������S�ʮڧY���Һc�����x�}���ڡA��Ѫk�Ȼݤ@�ӫ�²�檺���O�G
>> roots(p)
ans =
5.3723
-0.3723
�bMATLAB����̬O�h�m�h�����C��ڤW���F�W�[���P�u�@���K�Q�ʡA�����P��L�y���@�ˡA�]�p�����X��ơA�Ѧp�G sin, cos, log, exp, sqrt, �H�Ϋܦh�ܦh�C�ӱ`�����`�Ʀp��P�v pi,�ƼƤ� i �� j ���@�� -1�}��ڪ��N���H�A��eps�N���o�Ӽƾڥ@�ɤ��̤p���ȡA�����C�۫H�A�bMATLAB���@�ɤ��@�w�|���o�ܧּ֡A�����C
�h����
�bMatlab���A�@�Ӧh�����i�H�ΦV�q���N�C�G�p�n���ͤ@�Ӧh�����A�u�n�N��Y�ƨ̭�?�ƦC�m��@�ӦV�q�x�}���Y�i�C�]�A���b�B�z�U���@�Ӧh�����G
s4 + 3s3 - 15s2 - 2s +9
���ɧA�ߤ@�n�����ƬO�N�Y�ƨ̧ǩ�J�o�ӯx�}���G
>> x = [1 3 -15 -2 9]
x =
1 3 -15 -2 9
Matlab �|�N�o�@�� n+1�j�p���C�x�}�����@�� n ���褧�h�����C�G�Y�A�ҳB�z���h���������Y�Ƥ����̡A���m���O�d���s�A�H��o���T���x�}�V�q�A�Ҧp�G
s4 �@+�@��
��������G
y = [1 0 0 0 1]
���F�W�����x�}�V�q����A�A�i�H��polyval�o�Ө�ƨӨD�o�o�Ӧh��������ڭȡG�Ҧp�n�D�o��=2���h�����ȮɡA�i�U���O�p�U�G
z = polyval([1 0 0 0 1],2)
z =
17
�������~�A��i�M��䥿�T���ڡA�p�Ĥ@�Ӧh�����G
s4 + 3s3 - 15s2 - 2s +9
����O�p�U�G
>> roots([1 3 -15 -2 9])
ans =
-5.5745
2.5836
-0.7951
0.7860
�W���ڹ�ڤW�N�O�@�ӯx�}���S�x�x�}�ȡA�G�Y�ϥηR�ڭȩήڶ����ȥ�i�ϨD�h���Ƥ��Y�Ưx�}�A�o�ݭn�t�@�ӥspoly����ơG
?poly(ans)
ans =
1.0000 3.0000 -15.0000 -2.0000 9.0000
�p�G�A�ߦ�Ӽ�,�Q�N��Ӧh�����ۭ�,�o���G������matlab�A�����@�өҿפ��j��(convolution)���\��A�Q��conv��ƥi�H�N��Y�Ƭۭ��G
>> x = [1 2];
>> y = [1 4 8];
>> z = conv(x,y)
z =
1 6 16 16
�Ө�Ӧh�����۰��h��²��A��ϰj�۪��ӷ��\���ƥsdeconv�Y�i���Q�B�z�C�Ҧp���C���H�B�o��A�G.
>> [xx, R] = deconv(z,y)
xx =
1 2
R =
0 0 0 0
�P�e������,�䵲�G���P�e�z�ۦP�C�o�̤S���@����A�O�Ѱ����ɮɦs��l�ƪ���m�A�Y�ణ�ɫh�m��s�C
�Y�n��Ӧh���Ƭۥ[�A�����ϥίx�}�ۥ[�A���O�ۦw�L�ơA�u�O�x�}�ȯ�B�z��Ӧ�C�ۦP���x�}�C�Y�j�p���P�A�h�����ǧU�ۤv�w�q�����polyadd�C�ۤv�w�q�����M���|�bMATLAB���X�{�A���Y��ۤv�g�@�ӵ{���A�N����b�u��c���A�]��O�@���^�m�a�C�U���O���Ϊ��Ҥl�G
>> z = polyadd(x,y)
x =
1 2
y =
1 4 8
z =
1 5 10