Network Analysis, including PERT-CPM

網路分析

五種網路問題

 

 

a.    Finding the shortest route from an origin to a destination through a connecting network. 最短路徑

b.    Finding a set of connections that provide a route between any two points of the network in such a way as to minimize the total length of these connections. 最小展木

c.    Allocating flows to maximize the flow through a network connecting a source and a destination. 最大流量

d.    Minimum cost flow problem 最低總成本

e.    Project planning and control 計劃規劃與管制 - using PERT (計劃評核術) or CPM (要徑法)

      PERT: Program Evaluation and Review Technique

      CPM : Critical Path Method

 

 

 

9.1         標準範例


 


 

9.2         專有名詞

 

Components of typical networks網路的組成成分:

Nodes 節點

intersections, airports, switching points, pumping stations, work centers

Branches 分支

roads, air lanes, wires, channels, pipes, materials handling routes

Flow 流量

vehicles, aircraft, messages, fluid, jobs

 

Other terminology for describing graphs描述網路圖形:

Chain 鏈: 連接 ２ nodes 間的一系列 Branches 稱之

path 徑: 經過明定方向的 chain 稱之

cycle環

connected graph連圖  : 每對 nodes 皆有 chain 連接

 


 

 


tree木圖: connected graph but w/o cycle, N nodes with N-1 branches, (also named spanning tree) 展 木

 

 


 


oriented/directed branch, 有向枝: branch  w/ direction

oriented  graph, 有向圖 : 圖中之每一枝皆有向

flow capacity, arc capacity, 流通容量

supply node, source, 源點、起點：in < out

demand node, sink, 匯點、終點：in > out

transshipment node, 轉載點、中繼點：in = out

 

 

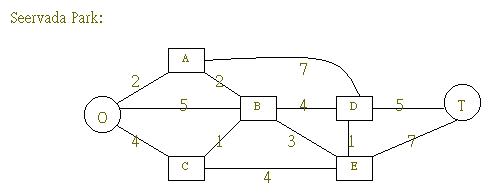
9.3         最短路徑問題 The shortest-route problem:

由入口O至Ｔ站之最短路線為何路徑 ?

 

目標 Objective：Find the shortest-length (least-cost) path associated w/ traveling from source to sink.

 

策略 Algorithm

策略 1

Start from SINK (Terminal) to SOURCE (origin)

Ｙi = ０   when i = 1  (sink, terminal)

Ｙi = MIN（Ｃij ＋　Ｙj）

for i = 2,3,4,...P, (P is total # of nodes)

only consider those nodes directly connected with j

 

What is Ｃij and what is Ｙj　？

 

Solution(Ｓ) : O - A - B - E - D - T or O - A - B - D - T

 

**  此 策略中的 MIN 改成 MAX 可用來求 longest route

策略 2:

Start from SOURCE to SINK，其他同策略1。

策略1與2 只適用於Acyclic network (對每一arc只有單一之流向者)。

 

策略3:

使用 LP 模式可解 General Network（node 與 node 間允許逆流）

Minimize  S Ｃij*Ｘij    (Ｘij 代表由 i 點流出至 j 點)

subject to

SＸkj －　 SＸik 　＝　1 　　for k = source

SＸkj －　 SＸik 　＝　0     for all other k

SＸkj －　 SＸik 　＝ -1     for k = sink

其中,  i,j,k  are nodes in network

例1：

for node O：ＸoA＋ＸoB＋ＸoC＝１

由上式可反推  node O 為source，流向 nodes A, B, C且為單向流。

例2：

for node 7：Ｘ72＋Ｘ73＋Ｘ76－Ｘ27－Ｘ87＝０

由上式可反推  node 7 為中繼點，非source 非sink，有流至nodes 2,3,6的 flow也有來自 nodes 2, 8的 flow。在 nodes 2與7中間允許逆流。

 

策略 4:

導出策略 3 LP模式 之Dual（對偶）模式，再求解 (仍為 LP 模式)

 

9.4         最小展木問題The minimum spanning tree problem

在所有各站間建立電話網路，欲使所需之線路為最短，應如何架設 ?

 

Algorithm:

 

1.        Start from any node, then connect it to the nearest node

2.        Identify the unconnected node that is closest to a connected node, and then connect these two. 在未連節點中找一點與任意已連節點之距離為最近者

3.        Repeat step 2 until all nodes are connected.

 

p.364 of your Text

 

 

 

9.5         最大流量問題The maximum flow problem

環保上之需求，每一路線所能允許之每日交通車來往次數有一上限，應如何排定交通車之路線，使不超過此上限且可運送之旅客數為最大 ?

 

This problem can also be formulated as a LP problem, so it can be solved by the simplex method, however, using Augmenting Path Algorithm is easier.

此問題可轉化為線性規劃模式，所以可用簡形法求解，但是用此章的解法較簡單。

 

目標: Maximize the flow from source to sink while subject to the limits on the flow capacity of each branch.

      Note: 同一 branch不同方向的 flow 可以有不同的上限

 

Algorithm:

 

1.   Identify the augmenting path by finding some directed path from source to sink in the residual network such that every arc on this path has strictly positive residual capacity (+RC). 全正流量徑. If none exist, you are done! Note：未明定方向之網路，以雙向視之，若只考慮其中一方向則稱之為  residual network.

2.   Search this path for the branch with the smallest remaining +RC (C*) and increase the flow in this path by C*. 找出該徑各枝流通容量之最小值，讓 C*量之流通過此徑。一徑之流通量 = 該徑各枝流通容量之最小值= 該徑可行流通容量之最大值

3.   Decrease by C* the remaining +RC of each arc in the path. Increase by C* the remaining RC in the opposite direction for each arc in the path.

4.   Go to step 1

 

 

Example: p.369, 370, 371 of your Text

 

*    Final CHECK !!

1.        初圖之各枝兩向流量之總和＝終圖之同一枝之兩向流量和

2.        初圖 sink + source之總和＝終圖 sink + source之總和

3.        初、終圖上相同之中運站各值之總和相等

*    比較初圖與終圖可得知：

1.        各枝之流向

2.        允許之各枝之最大流量

3.        允許之最大總流量

 

Some not-too-complicated problem can be solved using max-flow min-cut method. The theorem stated that, for any network with a single supply node and demand node, the maximum feasible flow from the supply node to the demand node equals the minimum cut value for all cuts of the network. 對於任意只有單一源點與匯點的最大可行流量為網路上所有切割的最小值

 

The cut value is the sum of the arc capacities of the arcs (in the specified direction) of the cut. A cut is any set of directed arcs containing at least one arc from every directed path from the source node to the demand node.

 

 

9.6         最低總成本問題Minimum cost flow problem

 

Like the maximum flow problem, it considers flow through a network with limited arc capacities.

 

Like the shortest path problem, it considers a cost for flow through an arc.

 

Like the transportation problem or assignment problem, it can consider multiple sources (supply nodes) and sinks (demand nodes) for the flow, with associated costs.

 

Like the transshipment problem, it also can consider various junction points between the sources and sinks for this flow.

 

數學模式 Formulation: Minimize 

subject to 受限於

 

         

     

      and   0 <= Xij <= Uij, for each arc i --> j

 

Feasible Solutions Property:

      A necessary condition for a minimum cost flow problem to have any feasible solutions is that: The total flow being generated at the supply nodes equals the total flow being absorbed at the demand nodes.

       

 

Integer solutions property:

For minimum cost flow problems where every ｂi and Uij has an integer value, all the basic variables in every basic feasible (BF) solution also have integer values.

 

Ref. Fig. 9.10 @ p.374

 

*   在限制式中，每個變數均有+1, -1 兩個係數

*   限制式中有一個為多餘的，此多餘者可為任意式子

 

特例 Special cases

 

Transportation Problem

1.   每個 source 皆為 Supply Node

2.   每個 sink   皆為 Demand Node

3.   NO Transshipment Nodes

4.   Ｕij= ∞, 代表不存在上限

Assignment Problem

同上，外加

1.   Number of supply nodes = number of demand nodes

2.   ｂi = 1 for each supply node

3.   ｂi =-1 for each demand node

Shortest Path Problem

1.   One supply node with a supply of 1

2.   One demand node with a demand of 1

3.   The rest of the nodes are transshipment nodes

4.   Ｕij = ∞

Maximum Flow Problem

1.   Ｃij= 0 for all existing arcs

2.   to assign a supply of a quantity Ｆto the supply node

3.   to assign a demand of a quantity Ｆto the demand node

4.   to add an arc from the supply node to the demand node and to assign it a large unit cost of Ｃij= Ｍ and an unlimited arc capacity （Ｕij= ∞）

Transshipment Problem

與 minimum cost flow problem 雷同，只差此者沒有  arc capacities. 基於此原因， minimum cost flow problem 又稱為 Capacitated Transshipment Problem.

 

 

9.7 網路簡形法Network Simplex Method

暫略

 

 

9.8 計劃規劃 Project scheduling by PERT-CPM (計劃評核術與要徑法)

 

良好的管理則需要有三個層次

Project scheduling by PERT-CPM consists of 3 basic phases: planning, scheduling and controlling. 大型計畫通常需要有良好的管理才可能成功，而良好的管理則需要：規劃、排訂行程（進度）、控制進度

     

Terminology of PERT

1.   Each branch of the project network represent an activity, which is one of the task required by the project. (branch=activity 活動, 欲完成計劃所必需從事的工作)

2.   Each node represents an event, which usually is defined as the point in time when all activities leading into that node are completed. (node=event, 進入該 node 之諸活動皆已完成的時間)

3.   Dashed line arrows, called dummies, show precedence relationships only; they do not represent any activities.(虛線為假想活動，只代表先後順序).

4.   Two Nodes can be directly connected by no more than 1 arc.

 

執行計劃評核的步驟

 

1st step:

Developing the network for a project 建立該專案計劃之網路圖

a. Identify all activities

b. Find out all the sequence

2nd step:

Estimate the time required for each of the activities. 估計各活動所需時間

T(i,j) is the activity time from event i to j.

3rd step:

Calculate two basic quantities for each event, namely, its earliest time and its latest time. 計算兩基本數值：最早時刻與最遲時刻

 

Earliest time (ET): the estimated time at which the event will occur if the proceeding activities are started as early as possible. 進入該 node之前的諸活動皆已完成的最早時間

ET(j) = max [ET(i)+T(i,j)]

 

Latest time (LT): the estimated last time at which the event can occur without delaying the completion of the project beyond its earliest time. 進入該 node 之諸活動皆必需完成的最晚時間

LT(i) = min [LT(j)-T(i,j)]

4th step:

Calculate the slack time of an event and the slack time of an activity.

 

Slack for an event 一事件之鬆弛（寬裕）時間: the difference between its latest and its earliest time.在不拖延整個計劃完成時間之先決條件下，該事件所能延遲的時間

 

Slack for an activity (i,j) 一活動之鬆弛（寬裕）時間: the difference  between the latest time of event j and (the earliest time of event  i  plus the estimated activity time). 不拖延該活動之完成，而所能延遲的時間

5th step:

Identify the critical path 找出要徑. A critical path for a project is a path through the network such that the activities on this path have zero slack （零鬆弛路線）.  A critical path is also a sequence of critical activities that must be kept strictly on schedule in order to avoid slippage in the project completion.

 

The PERT three estimate Approach計劃評核（PERT）三估計數法

 

In the previous example, the activity times are deterministic 確定的數值 (they can be reliably predicted without significant uncertainty). However, there usually is considerable uncertainty about what the time will be. 實務上此些數值通常涉及一些不確定因素所以很難確定

       

PERT uses three different types of estimates of the activity time to obtain basic information about its probability distribution.  The three time estimates are:

 

1.   the most likely estimate 最可能估計值 (m, peak of the probability  distribution), 

2.   the optimistic  estimate  最樂觀估計值 (a,  lower  bound  of the distribution),

3.   the pessimistic estimate  最悲觀估計值 (b,  upper  bound  of  the distribution).

       

Two assumptions are made to convert m, a, b into estimates of the expected value (期望值) and variance (變異數) of the elapsed time required by the activity.

 

1.      The standard deviation (square root of the variance) equals one sixth the range of reasonably possible time requirements,  ie.  (b-a)/6. The rationale for this assumption is that the tails of normal distribution are considered to lie at about 3 standard deviations from the mean.       

2.      The distribution of the time required for the activity is approximately b where the mode is ‘m’, the lower bound is ‘a’ and the upper bound is ‘b’ and st.d. is ‘(b-a)/6’. 活動之時間分佈大致依照b分佈曲線之模式

       

Estimated expected value (期望值) of elapsed time required for an activity (Te) = ( 4 m  + a + b ) / 6, 變異數 (Var) = (st.d)2

       

Three more assumptions required to enable the calculation of the probability of completing the project on schedule.   

1.            the activity times are statistically independent

2.            the critical path (in terms of expected times) always required a longer total elapsed time than any other path

3.            the project time has a normal distribution

 

Suppose the house-construction project is scheduled to completed after 50 working days and that both the estimated value and variance of each activity time happens to equal the estimated time given for that activity as shown in previous example. Therefore both the expected value and variance of the project time are 44, so its st.d. is 6.63.

             50-44 = 6 and 6/6.63 = 0.9

Thus the scheduled completion time is approximately 0.9 st.d. above the expected project time. From the table of normal distribution  (attached), one can find that the approximate probability that this schedule will be met is  1-0.1841 = 0.82

 

如期完工之機率：

 

假設築屋專案排定在50 天後完工且其期望值(EV) 與 變異數 (σ2) 與 前例之值相同，由前例之計算可知 EV= 44 天， σ2= 44 天，  √44 可得 標準差 (σ) 為  6.63. 依常態分佈之定義，在期望值+三個標準差(STD)的範圍內佔全數的99.73%，比EV-3*STD小或比EV+3*STD大的範圍則各佔0.135% (查p.970,Table A5.1常態分佈表之Kα=3.0, P{Normal> Kα}=0.00135)

 

在50 天後完工的機率為44+(50-44)/6.63 = EV + 0.9 個STD，(查Table A5.1, Kα=0.9, P{Normal> Kα}=0.1841)，在此範圍之外的機率為0.1841，所以如期完工的機率為1-0.1841 = 0.8159.

 

要徑法（CPM，包括時間與成本雙重考量）

The CPM method of Time-Cost Trade-Offs

 

*   CPM 法假設 activity times （Xij）are deterministic，而非如 PERT 法需要使用三估計數。

*   CPM 法強調時間與成本同等重要，而非如 PERT 法只考慮時間因素。

*   CPM 法如何強調時間與成本同等重要? Answer: 透過 Time-Cost Curve

 

   Time-Cost Curve of activity (i, j) 圖9.29 (p.400 of Textbook)

 

X: Activity duration time

Y: Activity direct cost

Normal Point

Normal Time Dij

Normal cost CDij

Crash Point

Crash Time dij

Crash cost Cdij

Normal point: 在不需增加任何成本之下，"工程"可以完成之時間。

Crash point: 在用盡所有可能之資源也不能使"工程"進度再提前完成之時間。

 

   The basic objective of CPM is to determine just which time-cost trade-off should be used for each activity to meet the scheduled project completion time at a minimum cost. 基本目標是找出每一活動在完成時間與所需成本上如何妥協以在預定的時間內完成所有活動且花費之總成本為最少。

 

Direct cost for activity (i,j) =  Kij+ Sij*Xij

其中，Kij 截距, Sij 斜率

Total direct cost for the project = Σ (Kij+ Sij*Xij) for all (i, j)

Maximize  Z(i,j) =  Σ(-Sij)*Xij  for all (i, j)

s.t.

Ｘij≧ｄij

Ｘij≦Ｄij

Ｙi +Ｘij-Ｙj <= ０

Ｙn<=Ｔ

 

Fig.9.30, p.403 provides a useful basis for a managerial decision on T when the important effects of the project duration (other than direct cost) are largely intangible.

 

When other effects are primary financial (indirect costs)， it is appropriate to combine the total direct cost curve and total indirect cost curve. （Fig. 9.31, p.404）

 

PERT/CPM 之變形

*   有一些 PERT 法僅使用單一估計數（Most Likely estimate）

*   PERT/COST 法則為PERT 法加上 CPM 之 time-cost trade-off 觀念

       統稱為 PERT type methods