Chap. 8、特殊的LP問題--運輸與指派問題
8.1 運輸問題 Transportation Problem
8.2 A Streamlined Simplex Method for the Transportation Problem
8.3 指派問題 The Assignment Problem
Transportation 與Assignment 問題為兩種重要的線性規劃問題,可有特殊的解法來求得啟始解。
8.1 運輸問題 Transportation Problem
假設某貨品在m個工廠生產後運往n個倉庫儲藏。若已知由某特定工廠運送1單位貨品至某特定倉庫之運輸成本,且若每一工廠之產能有一上限, 每一倉庫之存貨有一下限, 則運輸問題便是決定從每個工廠應運送多少單位的貨品到每個倉庫以使全部的運送成本在滿足特定的限制式之下為最小。
![]() = 從工廠 i 到倉庫 j 之運送量; i = 1,2,., m; j = 1,2,.,n.
= 從工廠 i 到倉庫 j 之運送量; i = 1,2,., m; j = 1,2,.,n.
![]() = 從工廠 i 運送 1單位到倉庫 j 之成本; i,j 同上
= 從工廠 i 運送 1單位到倉庫 j 之成本; i,j 同上
![]() = 倉庫 j 之最低需貨量; j = 1,2,....,n.
= 倉庫 j 之最低需貨量; j = 1,2,....,n.
![]() = 工廠 i 之產能; i = 1,2,..., m
= 工廠 i 之產能; i = 1,2,..., m
LP 模式: Minimize: ![]()
s.t.
![]() (1)
(1)
![]() (2)
(2)
![]()
由
(1) ![]()
由
(2) ![]()
![]()
若![]() , 則以上 (1), (2)之不等式將全改為等式。有可行解。
, 則以上 (1), (2)之不等式將全改為等式。有可行解。
Prototype
Example範例:
(p.305 of Text book)
P
& T 公司的運輸資料如下表
(紅框區為每車運輸成本)
|
m=3, n=4 |
倉庫1 |
倉庫2 |
倉庫3 |
倉庫4 |
產量 |
|
工廠1 |
464 |
513 |
654 |
867 |
75 |
|
工廠2 |
352 |
416 |
690 |
791 |
125 |
|
工廠3 |
995 |
682 |
388 |
685 |
100 |
|
分配量 |
80 |
65 |
70 |
85 |
SUM=300 |
Xij
為由工廠
i 至倉庫
j 之運載車數,目標函數為決定此12個決策變數之值,
Min. Z = 464 X11 + 513 X12
+ 654 X13 + 867 X14 + 352 X21 + 416 X22
+ 690 X23 + 791 X24 + 995 X31 + 682 X32
+ 388 X33 + 685 X34,
s.t.
|
X11
+ X12 + X13 + X14 |
|
|
=75 |
|
|
X21
+ X22 + X23 + X24 |
|
=125 |
|
|
|
X31+X32
+ X33 + X34 |
=100 |
|
X11
+ |
X21
+ |
X31 |
=80 |
|
X12 + |
X22 + |
X32 |
=65 |
|
X13
+ |
X23
+ |
X33
|
=70 |
|
X14+ |
X24+ |
X34 |
=85 |
|
Xij
>= 0 |
(i= 1,2,3; j=1,2,3,4) |
|
|
Example
– Production Scheduling (p.310)
某飛機製造商在四個月內每月有預定數量的噴射引擎需製造並完成安裝,若該月生產出比預定安裝數量多的引擎則需暫存於貨倉中,各月製造成本不同,相關數據如下表,請找出各月的最適當生產量使總成本為最小。
|
月份 |
預定安裝數量 |
最大生產量 |
製造的單位成本 |
儲存的單位成本 |
|
1 |
10 |
25 |
1.08 百萬 |
0.015百萬 |
|
2 |
15 |
35 |
1.11 |
0.015 |
|
3 |
25 |
30 |
1.1 |
0.015 |
|
4 |
20 |
10 |
1.13 |
|
|
Source
i: |
Production
of jet engines in month i (i=1,2,3,4) |
|
Destination
j: |
Installation
of jet engines in month j (j=1,2,3,4) |
|
Xij: |
Number
of jet engines produced in month i for installation in month j |
|
Cij: |
Cost associated with each unit of Xij =
cost per unit for production and any storage (if i<= j) |
|
Si
: |
Sum
of Xij for j=1,2,3,4 <= 各月的上限 |
|
dj: |
Number
of scheduled installations in month j. |
|
|
Cost per Unit Distributed |
Supply |
||||
|
Destination |
||||||
|
1 |
2 |
3 |
4 |
|||
|
Source |
1 |
1.08 |
1.08+0.015 |
1.08+2*0.015 |
1.08+3*0.015 |
? <=25 |
|
2 |
|
1.11 |
1.125 |
1.14 |
? <=35 |
|
|
3 |
|
|
1.1 |
1.115 |
? <=30 |
|
|
4 |
|
|
|
1.13 |
? <=10 |
|
|
Demand |
10 |
15 |
25 |
20 |
|
|
如前述總Demand 需等於總Supply才能有解,目前總Demand 為70,總Supply 的上限為100,差額為30,所以需透過Slack variable 的觀念產生一個需求量為30 的Dummy Demand,如此才滿足總Demand等於總Supply,如此才能有可行解。
|
|
Cost per Unit Distributed |
Supply |
|||||
|
Destination |
|||||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
Source |
1 |
1.08 |
1.095 |
1.11 |
1.125 |
0 |
25 |
|
2 |
M |
1.11 |
1.125 |
1.14 |
0 |
35 |
|
|
3 |
M |
M |
1.1 |
1.115 |
0 |
30 |
|
|
4 |
M |
M |
M |
1.13 |
0 |
10 |
|
|
Demand |
10 |
15 |
25 |
20 |
30 |
|
|
Example
–Distribution of water resource (p.312) - Metro water District Problem.
某水公司由三個河流引進水資源並提供四個都市,引水與賣水都需成本,各河流所能提供量與各都市之需求量及相關成本如下表:
|
|
Cost per Acre Foot |
Supply |
|||
|
都市1 |
都市2 |
都市3 |
都市4 |
||
|
河流1 |
16 |
13 |
22 |
17 |
50 |
|
河流2 |
14 |
13 |
19 |
15 |
60 |
|
河流3 |
19 |
20 |
23 |
--- |
50 |
|
Minimum
Need |
30 |
70 |
0 |
10 |
(in units of 1 million acre
feet) |
|
Requested |
50 |
70 |
30 |
|
|
都市4雖然要求的水量沒有上限,但基於現實的總Supply 為 (50+60+50)=160,且假設其他三個都市都僅提供其最少量 (30+70+0=100),則所結餘的(160-100=60)為都市4的上限量,以此值作為其Request 的量,所以上表的![]() 可用60來取代。
可用60來取代。
總Request (50+70+30+60=210)與總Supply (160) 的差額為50,假設存在另一條Dummy River 可提供50的量,且涉及的成本為0。依據上述的修改,新表如下所述:
Table
8.11 (p.314)
|
|
Cost per Acre Foot |
Supply |
|||
|
都市1 |
都市2 |
都市3 |
都市4 |
||
|
河流1 |
16 |
13 |
22 |
17 |
50 |
|
河流2 |
14 |
13 |
19 |
15 |
60 |
|
河流3 |
19 |
20 |
23 |
M |
50 |
|
河流4 (Dummy) |
0 |
0 |
0 |
0 |
50 |
|
Requested |
50 |
70 |
30 |
60 |
|
|
Min
needed |
30 |
70 |
0 |
10 |
|
由於都市1的需求下限為30,上限為50,而河流4 (Dummy)的供應量為50,且涉及成本為0,為了防止超過20以上的供應量來自河流4,且在滿足需求下限的諸來源中不能包括河流4(Dummy),在上表中需做適度的修改,如下表所示,將都市1的需求分為兩部分,其一為滿足最小需求量,且涉及河流4的成本為一大數M,再以剩餘的量20當作另一個新的需求量。
在都市4中,就算河流4(Dummy)的所有量50都給了都市4也不會超過其Demand 量,所以可不做如都市1的修改。
|
|
Cost per Acre Foot |
Supply |
||||||
|
都市1 |
都市1’ |
都市2 |
都市2’ |
都市3 |
都市3’ |
都市4 |
||
|
河流1 |
16 |
16 |
13 |
13 |
22 |
22 |
17 |
50 |
|
河流2 |
14 |
14 |
13 |
13 |
19 |
19 |
15 |
60 |
|
河流3 |
19 |
19 |
20 |
20 |
23 |
23 |
M |
50 |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
M |
0 |
0 |
50 |
|
Demand |
30 |
20 |
70 |
0 |
0 |
30 |
60 |
|
Demand為0的各欄可刪除,結果如下表:
Table
8.12 (p.315)
|
|
Cost per Acre Foot |
Supply |
||||
|
都市1 |
都市1’ |
都市2 |
都市3’ |
都市4 |
|
|
|
河流1 |
16 |
16 |
13 |
22 |
17 |
50 |
|
河流2 |
14 |
14 |
13 |
19 |
15 |
60 |
|
河流3 |
19 |
19 |
20 |
23 |
M |
50 |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
0 |
50 |
|
Demand |
30 |
20 |
70 |
30 |
60 |
|
8.2 A Streamlined Simplex Method for the Transportation Problem
以上所介紹的各個Example中傳統上若以 Simplex Method 求解,需面對 m + n +1列, (m+1) * (n+1) 行的表格。
依Prototype example 之例 m+n+1 = 3+4+1 = 8 列限制式, 其中 1 為 Row 0.
(m+1)*(n+1)
= m*n個決策變數+
(m+n) 個人工變數
+ 1 個rhs
= (3+1)*(4+1)=20.
由於Transportation 問題的特性,使用 Streamline Simplex Method 可將原Size 為 (m+n+1) by (m+1)*(n+1) 之問題簡化為 m by n 的問題。
Table 8.13 (p.316 of Text book)
|
|
|
|
|
mxn欄 |
m欄 |
n欄 |
1欄 |
|
|
基變數 |
列號 |
Z |
……Xij…… |
Zi…. |
Zm+j…… |
rhs |
|
1
列 |
Z |
0 |
-1 |
Cij |
M |
M |
0 |
|
m列 |
Zi |
1 i m |
0 |
1 |
1 |
|
Si |
|
n列 |
Zm+j |
m+1 m+j m+n |
0 |
1 |
|
1 |
dj |
在Zi之各列乘上 - ui, 在Zm+j之各列乘上 - vj, 加至列 0 可導出以下新列0:
Table 8.14 (p.316 of Text book)
|
|
基變數 |
列號 |
Z |
……Xij…… |
Zi…. |
Zm+j…… |
rhs |
|
1
列 |
Z |
0 |
-1 |
Cij-ui
- vj |
M-ui |
M- vj |
|
1.
基變數在列0的係數必為0 ,可令 Cij –ui
– vj = 0, 求出 ui 與 vj,人工變數在此無用。
2.
不需以rhs/入基變數在各列的係數值以找到出基變數,
3.
不需在簡算表中各列做任何代數處理以求得新的可行解,事實上,整個簡算表幾乎可省掉,只需保留Cij, Si,
dj 之資料。(所以此問題之尺寸可簡化為m x n)。
4.
需要一組可行基解作為計算之開始,若不使用人工變數,則需由以知的Cij, Si,
dj 資料中求出。
用來求出第一組可行基解的一般性原則:
1.
在現在所在的欄或列依據某種原則選取下一個基變數
2.
選取下一個基變數時要消耗掉適當的量使該列或該欄不再存在剩餘的Supply 或Demand.
3.
在後續的考量中刪除該列或欄。
4.
如果最後只剩下一列或一欄,則剩餘的每一變數皆為基變數
以下介紹三種方法用來求出第一組可行基解:
1.
西北角法
(NorthWest Corner Method)
2.
佛格近似法 (Vogel’s Approximation Method)
3.
羅瑟近似法 (Russell’s Approximation Method)
西北角法
選取X11(西北角)開始,由Supply 與Demand 之值中指定所能給的最大量,若Source i 有任何殘餘則選Xi,j+1 (右移一格)否則下移一格改選 Xi+1,j
Table
8.16 (p.320 of Text book)
|
|
Cost per Acre Foot |
Supply, ui |
||||
|
都市1 |
都市1’ |
都市2 |
都市3’ |
都市4 |
||
|
河流1 |
16 30 |
16 20 |
13 |
22 |
17 |
50 |
|
河流2 |
14 |
14 0 |
13 60 |
19 |
15 |
60 |
|
河流3 |
19 |
19 |
20 10 |
23 30 |
M 10 |
50 |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
0 50 |
50 |
|
Demand, vj |
30 |
20 |
70 |
30 |
60 |
Z=2470+10M |
佛格近似法
1.
由計算各行與各列之最小與次小者之差開始。
2.
選擇各行列中差數最大者。
3.
選擇差數最大之行或列中,單位成本最小者。
4.
將該行與該列中之Demand 與Supply 中之較小值指定給該變數,刪除該行或列。
5.
將對應之列/行之Supply/Demand 值扣除指定之值。
Table
8.17 (p.321 of Text book)
|
|
Destination |
Supply |
Row difference |
||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
河流1 |
16 |
16 |
13 |
22 |
17 |
50 |
3 |
|
河流2 |
14 |
14 |
13 |
19 |
15 |
60 |
1 |
|
河流3 |
19 |
19 |
20 |
23 |
M |
50 |
0 |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
0 |
50 |
0 |
|
Demand |
30 |
20 |
70 |
30 |
60 |
將30指定給X44 刪除Column 4 Supply4扣除30 |
|
|
Column
difference |
2 |
14 |
0 |
19 |
15 |
||
|
|
Destination |
Supply |
Row difference |
|||
|
1 |
2 |
3 |
5 |
|
|
|
|
河流1 |
16 |
16 |
13 |
17 |
50 |
3 |
|
河流2 |
14 |
14 |
13 |
15 |
60 |
1 |
|
河流3 |
19 |
19 |
20 |
M |
50 |
0 |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
20 |
0 |
|
Demand |
30 |
20 |
70 |
60 |
將20指定給X45 刪除Row 4 Demand 5 也扣除20 |
|
|
Column
difference |
2 |
14 |
0 |
15 |
||
|
|
Destination |
Supply |
Row Difference |
|||
|
1 |
2 |
3 |
5 |
|
|
|
|
河流1 |
16 |
16 |
13 |
17 |
50 |
3 |
|
河流2 |
14 |
14 |
13 |
15 |
60 |
1 |
|
河流3 |
19 |
19 |
20 |
M |
50 |
0 |
|
Demand |
30 |
20 |
70 |
40 |
將50指定給X13 刪除Row 1 Demand 3也扣除50 |
|
|
Column
difference |
2 |
2 |
0 |
2 |
||
|
|
Destination |
Supply |
Row Difference |
|||
|
1 |
2 |
3 |
5 |
|
|
|
|
河流2 |
14 |
14 |
13 |
15 |
60 |
1 |
|
河流3 |
19 |
19 |
20 |
M |
50 |
0 |
|
Demand |
30 |
20 |
20 |
40 |
將40指定給X25 刪除Column 5 Supply 2 扣除40 |
|
|
Column
difference |
5 |
5 |
7 |
M-15 |
||
|
|
Destination |
Supply |
Row Difference |
||
|
1 |
2 |
3 |
|
|
|
|
河流2 |
14 |
14 |
13 |
20 |
1 |
|
河流3 |
19 |
19 |
20 |
50 |
0 |
|
Demand |
30 |
20 |
20 |
將20指定給X23 刪除Row 2 Demand 3 扣除20 |
|
|
Column
difference |
5 |
5 |
7 |
||
|
|
Destination |
Supply |
Row Difference |
||
|
1 |
2 |
3 |
|
|
|
|
河流3 |
19 |
19 |
20 |
50 |
1 |
|
Demand |
30 |
20 |
0 |
Z=2460 |
|
|
Column
difference |
|
|
|
||
選取X31=30, X32=20, X33=0
羅瑟近似法
1.
計算各Row 與 Column 的最大數。
|
|
Destination |
Supply |
Row Row最大數, ui’ |
||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
河流1 |
16 |
16 |
13 |
22 |
17 |
50 |
22 |
|
河流2 |
14 |
14 |
13 |
19 |
15 |
60 |
19 |
|
河流3 |
19 |
19 |
20 |
23 |
M |
50 |
M |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
0 |
50 |
M |
|
Demand |
30 |
20 |
70 |
30 |
60 |
|
|
|
Column最大數 vj’ |
M |
19 |
M |
23 |
M |
||
2.
計算 Cij – ui’ – vj’ 。
3.
找絕對值最大的負數,選為為基變數。
|
|
Destination |
Supply |
ui’ |
||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
河流1 |
16-22-M |
16-22-19 |
13-22-M |
22-22-23 |
17-22-M |
50 |
22 |
|
河流2 |
14-19-M |
14-19-19 |
13-19-M |
19-19-23 |
15-19-M |
60 |
19 |
|
河流3 |
19-M-M |
19-M-19 |
20-M-M |
23-M-23 |
M-M-M |
50 |
M |
|
河流4 (Dummy) |
M-M-M |
0-M-19 |
M-M-M |
0-M-23 |
0-M-M |
50 |
M |
|
Demand |
30 |
20 |
70 |
30 |
60 |
|
|
|
vj’ |
M |
19 |
M |
23 |
M |
||
由上表可知Delta45=-2M 為絕對值最大的負數,X45為基變數。
4.
同佛格法之步驟4,指定min (Supply, Demand)給該變數(在此處為Supply=50較小,X45=50)。
5.
同佛格法之步驟5,刪除該列並將該欄之Demand扣除50 剩餘10。建立新表回Step 1重新計算。
6.
若最後只剩一列或一欄則所剩之值可直接指定給剩餘的變數。
新表如下所示:
|
|
Destination |
Supply |
Row Row最大數, ui’ |
||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
河流1 |
16 |
16 |
13 |
22 |
17 |
50 |
22 |
|
河流2 |
14 |
14 |
13 |
19 |
15 |
60 |
19 |
|
河流3 |
19 |
19 |
20 |
23 |
M |
50 |
M |
|
Demand |
30 |
20 |
70 |
30 |
10 |
|
|
|
Column最大數 vj’ |
19 |
19 |
20 |
23 |
M |
||
計算 Cij – ui’ – vj’ ,找絕對值最大的負數。
|
|
Destination |
Supply |
ui’ |
||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
河流1 |
16-22-19 |
16-22-19 |
13-22-20 |
22-22-23 |
17-22-M |
50 |
22 |
|
河流2 |
14-19-19 |
14-19-19 |
13-19-20 |
19-19-23 |
15-19-M |
60 |
19 |
|
河流3 |
19-M-19 |
19-M-19 |
20-M-20 |
23-M-23 |
M-M-M |
50 |
M |
|
Demand |
30 |
20 |
70 |
30 |
10 |
|
|
|
vj’ |
19 |
19 |
20 |
23 |
M |
||
由上表可知Delta15=-5-M 為絕對值最大的負數,指定Demand=10給該變數(X15=10),刪除該欄並將該列之Supply扣除10 剩餘40。新表如下所示:
|
|
Destination |
Supply |
Row Row最大數, ui’ |
|||
|
1 |
2 |
3 |
4 |
|
|
|
|
河流1 |
16 |
16 |
13 |
22 |
40 |
22 |
|
河流2 |
14 |
14 |
13 |
19 |
60 |
19 |
|
河流3 |
19 |
19 |
20 |
23 |
50 |
23 |
|
Demand |
30 |
20 |
70 |
30 |
|
|
|
Column最大數 vj’ |
19 |
19 |
20 |
23 |
||
計算 Cij – ui’ – vj’ ,找絕對值最大的負數。
|
|
Destination |
Supply |
ui’ |
|||
|
1 |
2 |
3 |
4 |
|
|
|
|
河流1 |
16-22-19 |
16-22-19 |
13-22-20 |
22-22-23 |
40 |
22 |
|
河流2 |
14-19-19 |
14-19-19 |
13-19-20 |
19-19-23 |
60 |
19 |
|
河流3 |
19-23-19 |
19-23-19 |
20-23-20 |
23-23-23 |
50 |
23 |
|
Demand |
30 |
20 |
70 |
30 |
|
|
|
vj’ |
19 |
19 |
20 |
23 |
||
由上表可知Delta13=-29 為絕對值最大的負數,指定Supply=40給該變數(X13=40),刪除該列並將該欄之Demand扣除40 剩餘30。新表如下所示:
|
|
Destination |
Supply |
Row Row最大數, ui’ |
|||
|
1 |
2 |
3 |
4 |
|
|
|
|
河流2 |
14 |
14 |
13 |
19 |
60 |
19 |
|
河流3 |
19 |
19 |
20 |
23 |
50 |
23 |
|
Demand |
30 |
20 |
30 |
30 |
|
|
|
Column最大數 vj’ |
19 |
19 |
20 |
23 |
||
計算 Cij – ui’ – vj’ ,找絕對值最大的負數。
|
|
Destination |
Supply |
ui’ |
|||
|
1 |
2 |
3 |
4 |
|
|
|
|
河流2 |
14-19-19 |
14-19-19 |
13-19-20 |
19-19-23 |
60 |
19 |
|
河流3 |
19-23-19 |
19-23-19 |
20-23-20 |
23-23-23 |
50 |
23 |
|
Demand |
30 |
20 |
30 |
30 |
|
|
|
vj’ |
19 |
19 |
20 |
23 |
||
由上表可知Delta23=-26 為絕對值最大的負數,指定Demand=30給該變數(X23=30),刪除該欄並將該列之Supply扣除30 剩餘30。新表如下所示:
|
|
Destination |
Supply |
Row Row最大數, ui’ |
||
|
1 |
2 |
4 |
|
|
|
|
河流2 |
14 |
14 |
19 |
30 |
19 |
|
河流3 |
19 |
19 |
23 |
50 |
23 |
|
Demand |
30 |
20 |
30 |
|
|
|
Column最大數 vj’ |
19 |
19 |
23 |
||
計算 Cij – ui’ – vj’ ,找絕對值最大的負數。
|
|
Destination |
Supply |
ui’ |
||
|
1 |
2 |
4 |
|
|
|
|
河流2 |
14-19-19 |
14-19-19 |
19-19-23 |
30 |
19 |
|
河流3 |
19-23-19 |
19-23-19 |
23-23-23 |
50 |
23 |
|
Demand |
30 |
20 |
30 |
|
|
|
vj’ |
19 |
19 |
23 |
||
由上表可知Delta21=-24 為絕對值最大的負數,指定Supply=30給該變數(X21=30),刪除該列並將該欄之Demand扣除30 剩餘0。新表如下所示:
|
|
Destination |
Supply |
Row Row最大數, ui’ |
||
|
1 |
2 |
4 |
|
|
|
|
河流3 |
19 |
19 |
23 |
50 |
23 |
|
Demand |
0 |
20 |
30 |
|
|
|
Column最大數 vj’ |
19 |
19 |
23 |
||
X31=0,
X32=20, X34=30
Table
8.18 (p.322 of Text book) 為以上計算過程之精簡版,結果彙整於Table 8.19。紅色數字顯示的格位,其為基變數,其組成為第一組BF solution.
Table
8.19(p.324of Text book)
|
|
Cost per Acre Foot |
Supply, ui |
||||
|
J=1 |
j=2 |
j=3 |
j=4 |
j=5 |
||
|
河流1 |
16 |
16 |
13 40 |
22 |
17 10 |
50 |
|
河流2 |
14 30 |
14 |
13 30 |
19 |
15 |
60 |
|
河流3 |
19 0 |
19 20 |
20 |
23 30 |
M |
50 |
|
河流4 (Dummy) |
M |
0 |
M |
0 |
0 50 |
50 |
|
Demand, vj |
30 |
20 |
70 |
30 |
60 |
Z=2570 |
比較:
1.
西北角法未使用 Cij 資料,所以求出的可行基解通常離最佳解較遠,需較多次的疊代運算 (iteration) 才能求出最佳解。
2.
佛格近似法較為通俗化,簡單,但程式碼較長。
3.
羅瑟近似法使用 Cij –ui – vj 的觀念求出第一組可行解,此改良使得程式碼可大幅簡化,因為與後續的求解可共用同一副程式。
以上三種方法請參見補充的軟體。
Optimality
test: A BF solution is optimal if and only if Cij-ui-vj >=0 for every (i,j)
such that Xij is nonbasic.
非基變數格之Cij-ui-vj >=0, 基變數格之Cij-ui-vj =0
所以 Cij=ui+vj for each (i,j) such that Xij
is basic.
由表8.19可知
|
X31: |
19=u3+v1 |
Set
u3=0, so v1=19 |
|
X32: |
19=u3+v2 |
So v2=19 |
|
X34: |
23=u3+v4 |
So v4=23 |
|
X21: |
14=u2+v1 |
Known
v1=19, so u2=5 |
|
X23: |
13=u2+v3 |
Known
u2=-5, so v3=18 |
|
X13: |
13=u1+v3 |
Known
v3=18, so u1=-5 |
|
X15: |
17=u1+v5 |
Known
u1=-5, so v5=22 |
|
X45: |
0=u4+v5 |
Known
v5=22, so u4=-22 |
8個方程式,9個未知數,第一個數用假設的其餘可求。
將此些u,v值代回表8.19 可求出每一格位的Cij-ui-vj,各基變數的Cij-ui-vj一定為0,可不用計算,求出各非基變數的Cij-ui-vj,整理如表8.20所示:
Table
8.19(p.324of Text book)
|
|
Cost per Acre Foot |
Supply, |
ui |
||||
|
j=1 |
j=2 |
j=3 |
j=4 |
j=5 |
|||
|
i=1 |
16 +2 |
16 +2 |
13 40 |
22 +4 |
17 10 |
50 |
-5 |
|
i=2 |
14 30 |
14 +0 |
13 30 |
19 +1 |
15 -2 |
60 |
-5 |
|
i=3 |
19 0 |
19 20 |
20 +2 |
23 30 |
M M-22 |
50 |
0 |
|
i=4 |
M M+3 |
0 +3 |
M M+4 |
0 -1 |
0 50 |
50 |
-22 |
|
i=5 |
30 |
20 |
70 |
30 |
60 |
Z=2570 |
|
|
vj |
19 |
19 |
18 |
23 |
22 |
|
|
Step
1. 若所有非基變數的Cij-ui-vj>=0
成立,則通過
Optimality Test. 否則選取絕對值最大的負數那格為Entering basic variable. 目前選取的為X25.
Step
2. 將Entering
B.V. 由0開始增加,其與同一列與同一欄的鄰近的基變數形成連鎖反應(Chain Reaction),增加的值在同一列或同一欄要予以扣除,使同樣滿足原來對Supply 與Demand 的限制。如表8.21所示。
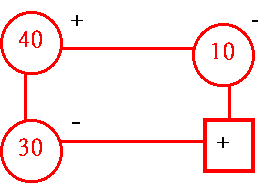
表8.21
|
|
Cost per Acre Foot |
Supply, |
|||
|
|
j=3 |
j=4 |
j=5 |
|
|
|
i=1 |
…… |
13 40 |
22 +4 |
17 10 |
50 |
|
i=2 |
…… |
13 30 |
19 +1 |
15 -2 + |
60 |
|
|
…… |
…… |
…… |
…… |
|
|
Demand |
|
70 |
30 |
60 |
|
X13, X25 為受贈格 (recipient
cells), X23, X15 為捐贈格 (donor
cells)。
捐贈與受贈的額度為 min (X23, X15)在此為min(30,10)=10,所以X15為Leaving B.V.,新舊值簡列如下表:
|
|
X13 |
X25 |
X23 |
X15 |
|
原值 |
40 |
0 |
30 |
10 |
|
新值 |
50 |
10 |
20 |
0 |
Step
3. The new BF solution 可透過Chain reaction 的計算求出。新的Z值亦可求出。
![]() Z = 10 (15-17+13-13) = 10 (-2) = 10 (C25 –u2-v5)
Z = 10 (15-17+13-13) = 10 (-2) = 10 (C25 –u2-v5)
The
effect of increasing the entering B.V. X25 from 0 has been a cost change at the
rate of –2 per unit increase in X25. This is preciously what the value of
C25-u2-v5 =-2 in Table 8.20 indicates would happen.
Summary
|
Initialization: |
以前述三種方法之任一者找出Initial BF solution |
|
Optimality
Test: |
找出 ui, vj, 求所有格位的 Cij-ui-vj,判斷是否所有的非基變數的Cij-ui-vj>=0 成立,若是,為最佳解,若不是,進入Iteration. |
|
Iteration: |
1.
決定Entering B.V. 2.
決定Leaving B.V. 3.
決定 new BF solution. 進入 Chain reaction. Chain
reaction 所選擇的鄰近的基變數必須再同一列或同一欄有可以抵消該變化的另一基變數存在時才可以選取。如Table 8.23 (p.330) Iteration
1 所示。 |
|
|
回Optimality Test (重新求ui, vj) |
參見Table
8.23 (p.330) 完成Metro water District Problem.
8.3 指派問題 The Assignment Problem
此亦為LP問題的特例,人員 (assignees)被指定從事某特定工作 (tasks) 且須滿足以下限制:
1.
The
number of assignees = number of tasks
2.
Each
assignee is to be assigned to exactly one task.
3.
Each
task is to be performed by exactly one assignee.
4.
There
is a cost Cij associated with assignee I (I=1,2,…,n) performing task j
(j=1,2,…, n).
5.
The
objective is to determine how all n assignments should be made in order to
minimize the cost.
標準範例 Prototype Example
JOB
SHOP 公司採購三種新機器,但有四個位置可以安裝,各機器在各位置涉及的搬運成本如表8.24所示:
|
|
Location
1 |
Location
2 |
Location
3 |
Location
4 |
|
Machine
1 |
13 |
16 |
12 |
11 |
|
Machine
2 |
15 |
-- |
13 |
20 |
|
Machine
3 |
5 |
7 |
10 |
6 |
如何安排此些機器使整體的搬運費用為最少?
Model
and Solution Procedures
Decision
variables: Xij = 1 if assignee i
performs task j, Xij =0 if not.
for
i and j = 1,2,…,n. Thus each Xij is a binary variable. (has value 0 or 1)
Minimize Z = total cost = ![]()
s.t. ![]()
![]()
and Xij >=0 (Xij binary, for all i and j)
與運輸問題的比較:
1.
number
of source m = number of supply n,
2.
every
supply Si =1, every demand dj=1
Figure
8.4 Network representation of the assignment problem. (p.334)
Table
8.26 (p.334)
|
|
Cost per Unit distributed |
supply |
|||
|
Location 1 |
Location 2 |
Location 3 |
Location 4 |
||
|
Machine 1 |
13 |
16 |
12 |
11 |
1 |
|
Machine 2 |
15 |
M |
13 |
20 |
1 |
|
Machine 3 |
5 |
7 |
10 |
6 |
1 |
|
Dummy (4) |
0 |
0 |
0 |
0 |
1 |
|
Demand |
1 |
1 |
1 |
1 |
|
Example
– Assigning Products to Plants
The BETTER PRODUCTS COMPANY 問題,如表8.27 (p.336)所示:
|
|
產品的單位成本 |
可用容量 |
|||
|
產品 1 |
產品 2 |
產品 3 |
產品 4 |
|
|
|
工廠 1 |
41 |
27 |
28 |
24 |
75件 |
|
工廠 2 |
40 |
29 |
-- |
23 |
75件 |
|
工廠 3 |
37 |
30 |
27 |
21 |
45件 |
|
所需生產速率 |
20 |
30 |
30 |
40 |
|
所需生產速率:Required production rate to meet
projected sales.
可用容量:Available production capacity of the
plants is measured by the number of units of any product that can be produced
per day.
各工廠可生產任意4種產品,只有工廠2無法生產產品3.
管理者面臨兩種選擇:
Option
1: 其一為允許不同工廠生產同一產品,
Option
2: 其二為不允許。
表8.28 (p.336). Option 1
|
|
產品的單位成本 |
可用容量 |
||||
|
產品 1 |
產品 2 |
產品 3 |
產品 4 |
5 (D) |
||
|
工廠 1 |
41 |
27 |
28 |
24 |
0 |
75 |
|
工廠 2 |
40 |
29 |
-- |
23 |
0 |
75 |
|
工廠 3 |
37 |
30 |
27 |
21 |
0 |
45 |
|
所需生產速率 |
20 |
30 |
30 |
40 |
75 |
|
|
答案: |
工廠 1生產產品 2, 3; 工廠 2生產37.5%的產品 4; 工廠 3生產62.5%的產品4 與產品1. |
表8.29 (p.337). Option 2
|
Task Assignee |
產品的單位成本 |
||||
|
產品 1 |
產品 2 |
產品 3 |
產品 4 |
5 (D) |
|
|
工廠 1a |
41*20 |
27*30 |
28*30 |
24*40 |
0 |
|
工廠 1b |
41*20 |
27*30 |
28*30 |
24*40 |
0 |
|
工廠 2a |
40*20 |
29*30 |
M |
23*40 |
0 |
|
工廠 2b |
40*20 |
29*30 |
M |
23*40 |
0 |
|
工廠 3 |
37*20 |
30*30 |
27*30 |
21*40 |
M |
|
答案: |
工廠 1生產產品 2, 3; 工廠 2生產產品 1; 工廠 3生產產品4. |
另一種Assignment 問題:旅行推銷員問題Traveling Salesman Problem
五個城市間的距離如下表所示,由任一城市出發,要走遍所有城市並回到起始城市,請找出有最短總距離的路線,最短總距離為多少?
|
|
City 1 |
City 2 |
City 3 |
City 4 |
City 5 |
|
City 1 |
|
42 |
30 |
30 |
25 |
|
City 2 |
42 |
|
30 |
30 |
18 |
|
City 3 |
30 |
30 |
|
42 |
25 |
|
City 4 |
30 |
30 |
42 |
|
18 |
|
City 5 |
25 |
18 |
25 |
18 |
|
此題可看成如下問題:
|
|
Task 1 |
Task 2 |
Task 3 |
Task 4 |
Task 5 |
|
Assignee 1 |
|
42 |
30 |
30 |
25 |
|
Assignee 2 |
42 |
|
30 |
30 |
18 |
|
Assignee 3 |
30 |
30 |
|
42 |
25 |
|
Assignee 4 |
30 |
30 |
42 |
|
18 |
|
Assignee 5 |
25 |
18 |
25 |
18 |
|
其中Assignee n 不能執行 task n.
補充閱讀 -- 線性規劃在農業上的應用實例
Fang, W., K.C. Ting and G.A. Giacomelli. 1990. Optimizing Resource Allocation for Greenhouse Potted Plant Production. Transactions of the ASAE, 33(4): 1377-1382. 溫室內盆栽作物生產相關資源配置之最佳化分析