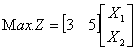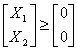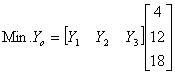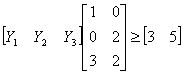Chap.6. �ﰸ�z�P�ӷP�פ��R
6.1 �ﰸ�z�ת�����
���D���D�����Y Primal-Dual relations
|
���D Primal Problem |
���D Dual Problem |
|
|
|
|
s.t.
|
s.t.
|
|
�p�������=m2n |
�p�������= n2m �]��m���j�ɦ��Q�^ |
�x�}���ܪk
|
Max Z �� C X s.t. A X <= b X >= 0 |
Min Yo �� Y b s.t. Y A >= C Y >= 0 |
|
��i���ܦp�U�G |
|
|
Min ��T�� s.t. �Ϣ� <= �� �� >= �� |
Max ��T�� s.t. ��T �� >= C �� >= �� |
|
Ex: p.198 Table 6.1 |
|
|
s.t.
|
s.t.
|
���D���D�m��
Ex1:
|
���D |
���D |
|
MAX 20 A + 30 C SUBJECT TO A <= 60 C <= 50 A + 2 C <= 120 END |
MIN 60 X + 50 Y + 120 Z SUBJECT TO 1 X + 1 Z >= 20 1 Y + 2 Z >= 30 END |
|
O.F.V. 2100.00
VARIABLE VALUE Reduced Cost A 60 0 C 30 0
ROW SLACK Dual Prices 2) 0 5 3) 20 0 4) 0 15 |
O.F.V. 2100.00
VARIABLE VALUE Reduced Cost X 5 0 Y 0 20 Z 15 0 ROW SLACK 2) 0 -60 3) 0 -30 |
Ex2:
|
���D MAX 4 X - 2 Y SUBJECT TO 2 X + 6 Y <= 12 3 X - 2 Y �� 1 4 X + 2 Y >= 5 END |
���D���ܫ� MAX 4 X - 2 Y SUBJECT TO 2 X + 6 Y <= 12 ơ 3 X - 2 Y <= 1 ơ -3 X + 2 Y <= -1 ơ -4 X - 2 Y <= -5 END |
|
�[���G 3 X - 2 Y ��1 �i���� 3 X - 2 Y >= 1�P 3 X - 2 Y <=1�⦡�P�ɦ��ߡA�S>=������P���H-1�i�אּ<=���������C |
|
|
���D |
|
|
MIN 12 R + S - T - 5 U SUBJECT TO 2 R + 3 S - 3 T - 4 U >= 4 6 R - 2 S + 2 T - 2 U >= -2 END |
|
Table 6.2 Primal-Dual Table for LP, illustrated by the Wyndor Glass Co. Example.
Table 6.3 Correspondence between Entitties in Primal and Dual Problems
|
One Problem |
|
Other Problem |
|
Constraint i |
ßà |
Variable i |
|
Objective func. |
ßà |
Right Sides |
²��k���믫�b��M�@�հ��ܼƻP�۹�����BF Solution, �ϱorow 0 ���Ҧ��Y�Ƨ����D�t�C
Condition
for Optimality�G
Zj - Cj >= 0,
for j = 1, 2, 3,�K., n,
Yi >= 0, for I = 1,
2,3,�K.., m.
Table 6.4 Notation for Entries in row 0 of a simplex Tableau
|
|
|
|
Coefficient of: |
|
||||||||
|
Iteration |
Basic Var. |
Eq. |
Z |
X1 |
X2 |
�K. |
Xn |
Xn+1 |
Xn+2 |
�K. |
Xn+m |
Right side1 |
|
any |
Z |
0 |
1 |
Z1-C1 |
Z2-C2 |
�K. |
Zn-Cn |
y1 |
y2 |
�K. |
ym |
y0 |
Table 6.5 Row 0 and corresponding dual solution for each iteration for the Wyndor glass Co. example.
|
iteration |
Primal Problem |
Dual Problem |
y0 |
|||||||||
|
Row 0 |
y1 |
y2 |
y3 |
Z1- C1 |
Z2- C2 |
|||||||
|
0 |
-3 |
-5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-3 |
-5 |
0 |
|
1 |
-3 |
0 |
0 |
5/2 |
0 |
30 |
0 |
5/2 |
0 |
-3 |
0 |
30 |
|
2 |
0 |
0 |
0 |
3/2 |
1 |
36 |
0 |
3/2 |
1 |
0 |
0 |
36 |
Z* = 36 = y0*
�z�ﰸ�ʡA�j�ﰸ�ʡA���ɩʡA�ι�٩�
![]() �z�ﰸ�ʡGX�����D���i��ѡAY�����D���i��ѡA�hC X <= Y b
�z�ﰸ�ʡGX�����D���i��ѡAY�����D���i��ѡA�hC X <= Y b
![]() �j�ﰸ�ʡGX*�����D�����u�ѡAY*�����D�����u�ѡA�hC X*=Y* b
�j�ﰸ�ʡGX*�����D�����u�ѡAY*�����D�����u�ѡA�hC X*=Y* b
Note that�G
���D��Max ���D�A�s�bC X <= C X*
���D��Min ���D�A�s�bY b >= Y* b
![]() ���ɩʡG�b²��k���C�����Эp�⤤�A�i�D�o���D���i��ѻP���D�����ɸ�
(�b�C0���A���t�B�ܼƪ��Y��)�A�䤤 C X=Y b�C�YX���O���D�����u�ѡA�hY�礣�O���D���i��ѡC
���ɩʡG�b²��k���C�����Эp�⤤�A�i�D�o���D���i��ѻP���D�����ɸ�
(�b�C0���A���t�B�ܼƪ��Y��)�A�䤤 C X=Y b�C�YX���O���D�����u�ѡA�hY�礣�O���D���i��ѡC
![]() ���ɳ��u�ʡG�b�̫�@�������Эp��ɡA²��k�i�P�ɨD�X���D�����u��X*�P���D�����ɳ��u��Y*�A�䤤
C X*=Y* b�AY*��Yi*�զ��A�Y���v���C
���ɳ��u�ʡG�b�̫�@�������Эp��ɡA²��k�i�P�ɨD�X���D�����u��X*�P���D�����ɳ��u��Y*�A�䤤
C X*=Y* b�AY*��Yi*�զ��A�Y���v���C
![]() ��٩ʡG���D�����D�����D
��٩ʡG���D�����D�����D
Duality Theorem�G
1.
�Y�Y���D�ΰ��D���i��ѥB�����ɪ��ؼШ�ơA�������A�|���̨θѮɡA�h����������D�έ��D�]�|���̨θѡA�B�z��٩ʻP�j��٩ʧ��A�ΡC
2.
�Y�Y���D�ΰ��D���i��Ѧ��ؼШ�Ƭ��L�ɮɡA�������A�S���̨θѮɡA�h����������D�έ��D�N�䤣��i��ѡC
3.
�Y�Y���D�ΰ��D�L�i��ѮɡA�h����������D�έ��D���O�S���i��ѡA�N�O��ؼШ�Ƭ��L�ɡA�`���A�N�䤣��̨θѡC
Table 6.7 Association between variables in Primal and Dual problems
|
Primal variable |
Associated Dual variable |
|
Original vari. Xi |
Zj - Cj (surplus vari.) j = 1,2,�K,n |
|
Slack vari. Xn+1 |
yi (original vari.) i=1,2,..,m |
Table 6.10 Classification of Basic solutions (p.210)
|
|
Satisfies Condition for Optimality |
||
|
Yes |
No |
||
|
Feasible ? |
Yes |
Optimal |
Suboptimal |
|
No |
Superoptimal |
Neither feasible Nor Superoptimal |
|
Basic solutions �i�Ψ�ؤ覡�Ӥ����A���O���O�_�i�� (condition for feasibility) �P�O�_���̨� (condition for optimality)�C�e�̳z�L�X�R�Ѥ����Ҧ��ܼƬO�_���D�t(0�Υ���)�ӧP�_�A��̳z�L�b�C0���Y�ƬO�_�����D�t�ƨӧP�_�C

Table 6.11
|
Primal basic solution |
Complementary Dual basic solution |
|
Suboptimal |
Superoptimal |
|
Optimal |
Optimal |
|
Superoptimal |
Suboptimal |
|
Neither feasible not superoptimal |
Neither feasible not superoptimal |
Table 6.13 Constructing the Dual of the Dual Problem
|
Dual Problem |
|
Converted to standard Form |
|
Minimize yo= y b s.t. y A >= c and y >= 0 |
à |
Maximize (-yo)= -y b s.t. -y A <= - c and y >= 0 |
|
|
||
|
Converted to standard Form |
|
Its Dual Problem |
|
Maximize Z = c X s.t. A X <= b and X >= 0 |
ß |
Minimize (-Z) = -c X s.t. -A X >= - b and X >= 0 |
Table 6.14 Corresponding Primal-Dual forms
|
Primal Problem (or Dual Problem) |
Dual Problem (or Primal Problem) |
||
|
Maximize Z (or yo) |
Minimize yo (or Z) |
||
|
��� i�G |
�ܼ� yi
(or Xi)�G |
||
|
<= |
Form |
|
yi >= 0 |
|
= |
Form |
|
unconstrainted |
|
>= |
Form |
|
yi
'<= 0 |
|
�ܼ� Xj (or yj)�G |
��� j�G |
||
|
|
Xj >= 0 |
>= |
Form |
|
|
unconstrainted |
= |
Form |
|
|
Xj
'<= 0 |
<= |
Form |
Table 6.15 One Primal-Dual Form for the Radiation Therapy Example
|
Primal Problem |
|
Dual Problem |
|
Maximize -Z=-0.4X1-0.5X2 s.t. 0.3X1+0.1X2<=2.7 0.5X1+0.5X2=6 0.6X1+0.4X2>=6 and X1>=0 X2>=0 |
|
Minimize yo=2.7y1+6y2+6y3' s.t. y1>=0 y2 unconstrainted in sign y3'<=0 and 0.3y1+0.5y2+0.6y3'>=-0.4 0.1y1+0.5y2+0.4y3'>=-0.5 |
6.6 �ӷP�פ��R Sensitivity analysis
Table 6.18
|
|
Basic Var. |
Eq. |
Coefficient of: |
r.h.s. |
|||||
|
Z |
x1 |
x2 |
x3 |
x4 |
x5 |
||||
|
New initial tableau |
Z |
(0) |
1 |
-4 |
-5 |
0 |
0 |
0 |
0 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
|
|
x4 |
(2) |
0 |
0 |
2 |
0 |
1 |
0 |
24 |
|
|
x5 |
(3) |
0 |
2 |
2 |
0 |
0 |
1 |
18 |
|
���s����Y�bc1, a31, b2 ���F�C
���D���̥�����
|
Final tableau for original model |
Z |
(0) |
1 |
0 |
0 |
0 |
3/2 |
1 |
36 |
|
x3 |
(1) |
0 |
0 |
0 |
1 |
1/3 |
-1/3 |
2 |
|
|
x2 |
(2) |
0 |
0 |
1 |
0 |
1/2 |
0 |
6 |
|
|
x1 |
(3) |
0 |
1 |
0 |
0 |
-1/3 |
1/3 |
2 |
�̨θѬ� (2, 6), Z = 36
Table 6.17 (p.219)
|
Revised final tableau |
Z |
(0) |
1 |
z*- |
y* |
Z* |
|
x3 |
(1) |
0 |
A* |
S* |
b* |
|
|
x2 |
(2) |
0 |
||||
|
x1 |
(3) |
0 |
�ץ��D���̥�����
|
Revised final tableau |
Z |
(0) |
1 |
-2 |
0 |
0 |
3/2 |
1 |
54 |
|
x3 |
(1) |
0 |
1/3 |
0 |
1 |
1/3 |
-1/3 |
6 |
|
|
x2 |
(2) |
0 |
0 |
1 |
0 |
1/2 |
0 |
12 |
|
|
x1 |
(3) |
0 |
2/3 |
0 |
0 |
-1/3 |
1/3 |
-2 |
Table 6.19�ץ��D���̥�����z�LGaussian elimination �A���H�ץ�
|
|
Basic Var. |
Eq. |
Coefficient of: |
r.h.s. |
|||||
|
Z |
x1 |
x2 |
x3 |
x4 |
x5 |
||||
|
Converted to proper form |
Z |
(0) |
1 |
0 |
0 |
0 |
1/2 |
2 |
48 |
|
x3 |
(1) |
0 |
0 |
0 |
1 |
1/2 |
-1/2 |
7 |
|
|
x2 |
(2) |
0 |
0 |
1 |
0 |
1/2 |
0 |
12 |
|
|
x1 |
(3) |
0 |
1 |
0 |
0 |
-1/2 |
1/2 |
-3 |
|
�bc1, a31, b2 ���F����A�W�C����i�D�ڭ̨̳θѥѭ�Ӫ� (2, 6) �אּ (-3, 12)�A�ӫ�̥ѩ�b���ܼƤ���x1 ���t�ơA�ҥH�Ӹ��ܬ� non-feasible�A���ѩ�C0 ���Ҧ��Y�Ƨ����D�t�A�ҥH�亡��optimality test�C��Table 6.10 �i����basic solution ��Superoptimal�C�i�i�@�B�b��Dual simplex method �D�ѡC
Summary of procedure for Sensitivity Analysis
1. Revision of model
2. Revision of final tableau
3. Conversion to proper form from Gaussian elimination
4. Feasibility test
5. Optimality test
6. Reoptimization
6.7 Applying Sensitivity Analysis
(�ɥR���e)
���T�譱�ӱ��Q�G����1.�ؼШ�ƪ��Y�ƭȪ��ܰʡA2.����������Y�ƭȪ��ܰʡA3.�䥦��������� rhs �Ȫ��ܰ� (�]�A��ڸ�T�B�P�䥦)�C
�ؼШ�ƪ��Y�ƭȪ��ܰ�
|
100 % Rule by Bradley, Hax and Magnanti (1977): Any combination of change will not change the basis�]�^if the sum of the percentages of slack used sums to less than 100%. |
|
the % of slack =�ؼШ�ƪ��Y�ƪ��ܰʶq/allowable decrease or increase |
|
�d�ҡG MAX 20 A + 30 C -----> 17 A + 20 C SUBJECT TO 2) A <= 65 3) C <= 50 4) A + 2 C <= 120 END |
|
O.F.V. = 2100 �B A = 60�A C = 30 |
�H LINDO �@�ӷP�פ��R���������G�p�U���G
|
VARIABLE |
CURRENT COEF. |
ALLOWABLE INCREASE |
ALLOWABLE DECREASE |
|
A |
20 |
INFINITY |
5 |
|
C |
30 |
10 |
30 |
|
100 % Rule�G (20-17)/5 + (30-20)/30 = 0.6 + 0.333 = 0.933 < 100 % |
|
Basis ���ܡA A = 60�A C = 30 --> new O.F.V. = 2100 - 60 * 3 - 30 * 10 = 2100 - 480 = 1620 |
������Y�ƭȪ��ܰ�
|
O.F.V.�ﵽ�q =(value of variable j) x (dual price of row i) x e �䤤�A e �� row i �� variable j ���Y�ƪ���֪��L�p�� |
|
�d�ҡG |
|
MAX 20 A + 30 C SUBJECT TO 2) A <= 65 3) C <= 50 4) A + 2 C <= 115 -->��אּA + 2.01 C <= 115 END O.F.V. = 2050.00 |
|
VARIABLE VALUE REDUCED COST A 65 0 C 25* 0 ROW SLACK DUAL PRICES 2) 0 5 3) 25 0 4) 0 15* |
|
�w���� O.F.V. = 2050 + (25*15*(-0.01)) = 2050 - 3.75 = 2046.25 �u���� O.F.V. = 2046.269, O.F.V. decrease by 3.731 |
��ڸ�T�]Marginal Information�^
|
��ڸ�T�]�A�G��ڦ����]Marginal Cost�^�P��ڻ��ȡ]Marginal Value�^�A���G�W�����O�P LINDO ���ϥΪ�Reduced Cost��Dual Prices �۳q�C |
|
������ Reduced Cost �P Dual Prices �����Q�A�аѦҡyLP�ɥR�Ч��z���� LINDO �i���C |
��������� rhs �Ȫ��ܰ�
![]() �W�[ '<=���'�� rhs �Ȫ��ܩ��P����d��A�u�i���v�]feasible
domain�^�N�X�j�A�ؼШ�ƭȡ]O.F.V.�^�i��W�[�C
�W�[ '<=���'�� rhs �Ȫ��ܩ��P����d��A�u�i���v�]feasible
domain�^�N�X�j�A�ؼШ�ƭȡ]O.F.V.�^�i��W�[�C
![]() ��� '<=���'�� rhs �ȡA �ؼШ�ƭȥi���֡C
��� '<=���'�� rhs �ȡA �ؼШ�ƭȥi���֡C
![]() �W�[ '>=���'�� rhs �Ȫ��ܥ[�j����d��A�u�i���v�N�Y�p�A�ؼШ�ƭȥi���p�C
�W�[ '>=���'�� rhs �Ȫ��ܥ[�j����d��A�u�i���v�N�Y�p�A�ؼШ�ƭȥi���p�C
![]() ��� '>=���'�� rhs �ȡA�ؼШ�ƭȥi��W�[�C
��� '>=���'�� rhs �ȡA�ؼШ�ƭȥi��W�[�C
![]() �W�[ '=���'�� rhs �Ȫ��ܲ�����ɡ]Boundary�^�A�ؼШ�ƭȥi��[�j�i���p�C
�W�[ '=���'�� rhs �Ȫ��ܲ�����ɡ]Boundary�^�A�ؼШ�ƭȥi��[�j�i���p�C
![]() ��� '=���'�� rhs �ȡA �ؼШ�ƭȥi��[�j�i���p�C
��� '=���'�� rhs �ȡA �ؼШ�ƭȥi��[�j�i���p�C
�P Dual Prices ���[�����X�G
|
�� Dual Prices ���� �� 0 �ɡA��۹����� SLACK or SURPLUS �� 0�A���ܸӭ���w�Ψ췥�I�]�f�y�ƻ��k�^�A�Y��W�[ rhs ���ȡA�h O.F.V. �i�W�[�P Dual Price �ۦP���q�C |
�[�J�s�ܼƩηs���
�[�J�s�ܼƩηs������ɬO���n���Ҷq�A
![]() �s�ܼơG�ݩ�m��Ҧ��������B�A�]�A�ؼШ�ƤΦU����A�s�ܼƦb�ؼШ�ƤΦU������A�Τ��Y�ƥ�ݥ[�H�Ҷq�C
�s�ܼơG�ݩ�m��Ҧ��������B�A�]�A�ؼШ�ƤΦU����A�s�ܼƦb�ؼШ�ƤΦU������A�Τ��Y�ƥ�ݥ[�H�Ҷq�C
![]() �s����G�i��O��ӬG�N���[�Ω������[�A�ӷP�פ��R���ɯA�ηs����A�����D���L���h�ѡ]unbounded�^�ɡA�`�`�O�]�Y�@���n����Q�����F�C
�s����G�i��O��ӬG�N���[�Ω������[�A�ӷP�פ��R���ɯA�ηs����A�����D���L���h�ѡ]unbounded�^�ɡA�`�`�O�]�Y�@���n����Q�����F�C
(�Ь�Ѥ��e)
Case 1 changes in bi (p.224)
One or more of the ��right hand side�� values have been changed.
Right side of final row 0:![]()
Right side of final rows 1,2,�K,m: ![]()
�ҡG�Nb = [4 12 18]T �אּ à ![]() [4 24 18]T
[4 24 18]T
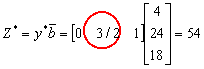
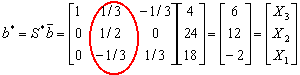
�ҡGb2 ��12 �אּ24
|
Max. |
3X1 + 5 X2 |
|
|
s.t. |
X1 <=4 2X2<=24 3X1+2X2 <=18 X1, X2 >=0 |
|
Table 6.20 Revised data for Wyndor glass Co. problem after just b2 is changed.
|
|
BasicVar. |
Eq. |
Coefficient of: |
r.h.s. |
|||||
|
Z |
x1 |
x2 |
x3 |
x4 |
x5 |
||||
|
Final tableau after reoptimization |
Z |
(0) |
1 |
9/2 |
0 |
0 |
0 |
5/2 |
45 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
3/2 |
1 |
0 |
0 |
1/2 |
9 |
|
|
x4 |
(3) |
0 |
-3 |
0 |
0 |
1 |
-1 |
6 |
|
�t�k�G�u�Ҽ{����諸���(2nd
column of S*)�P�A�Ϊ��ܼ�(2nd component of y*)�A![]() �ҥHZ = ���36+18=54
�ҥHZ = ���36+18=54
|
|
à |
|
|
|
à |
|
|
|
à |
|
![]()
This range of values for b2 is referred to allowable range to stay feasible.
Case 2a. Changes in the coefficients of a Nonbasic variables
Refer to Table 6.20 of p.226, x3, x2, x4 �����ܼơAx1�P x5���D���ܼơC
�ѩ�D���ܼƤ��Ȧbbasic solution ����Ȭ�0�A�ק�U�Y�ƨ�ꤣ�|��̨έȦ��v�T�A�u�ݽT�{�ӭȬO�_�����̨θѡC
�ҡG
|
Max. |
3X1 + 5 X2 �ץ��� |
4X1 + 5 X2 |
|
s.t. |
X1 <=4 2X2<=24 3X1+2X2 <=18 X1, X2 >=0 |
X1 <=4 2X2<=24 2 X1 + 2 X2 <=18 X1, X2 >=0 |
|
���D |
Max Z = CX s.t. A X <= b |
|
|
���D |
Min y0=y b s.t. yA >= C |
|
|
|
Min y0=[y1* y2* y3*]T [4 24 18] s.t. [y1* y2* y3*]T [1 0 3] >=3 [y1* y2* y3*]T [0 2 2] >=5 |
|
|
�ץ��᭭� |
s.t. [y1* y2* y3*]T [1 0 2] >=4 |
|
�ѤW���i���A�����D���D���ܼƪ��Y�Ƭ۹��䰸�D�Ө��A�u��@�ӭ�����v�T�A�ҥH�Y���D y* �����s������A�h���D���̨θѦb�ץ��ᤴ���̨θѡC
The allowable range to stay optimal
���� Cj <= y* Aj
Case 2b. Introduction of a New variable
���]���D���h�F�@�ӫD���ܼơA��Y�ƬҬ�0�A�A��Case 2a ���覡�h�ץ��Y�ơC
Case 3. Changes in the Coefficients of a Basic variable
�ҡG
|
Max. |
3X1 + 5 X2 �ץ��� |
3X1 + 3 X2 |
|
s.t. |
X1 <=4 2X2<=24 3X1+2X2 <=18 X1, X2 >=0 |
X1<=4 3X2 <=24 3X1 + 4 X2 <=18 X1, X2 >=0 |
Table 6.21
|
|
BasicVar. |
Eq. |
Coefficient of: |
r.h.s. |
|||||
|
Z |
x1 |
x2 |
x3 |
x4 |
x5 |
||||
|
Revised final tableau |
Z |
(0) |
1 |
9/2 |
7 |
0 |
0 |
5/2 |
45 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
3/2 |
2 |
0 |
0 |
1/2 |
9 |
|
|
x4 |
(3) |
0 |
-3 |
-1 |
0 |
1 |
-1 |
6 |
|
|
Converted to proper form |
Z |
(0) |
1 |
-3/4 |
0 |
0 |
0 |
3/4 |
27/2 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
3/4 |
1 |
0 |
0 |
1/4 |
9/2 |
|
|
x4 |
(3) |
0 |
-9/4 |
0 |
0 |
1 |
-3/4 |
21/2 |
|
|
After reoptimization (0ne iteration of the simplex method) |
Z |
(0) |
1 |
0 |
0 |
3/4 |
0 |
3/4 |
33/2 |
|
x1 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
0 |
1 |
-3/4 |
0 |
1/4 |
3/2 |
|
|
x4 |
(3) |
0 |
0 |
0 |
9/4 |
1 |
-3/4 |
39/2 |
|
Case 4. Introduction of a New constraint
|
Step 1. |
�b��Simplex Method ���̥����椤�[�J�s������A�ϥηs��Slack or Artificial variable. |
|
Step 2. |
�ഫ���A�����榡 |
|
Step 3. |
����̨θ��ܬ�Superoptimal �ɡA�ϥ�Dual Simplex Method �ӭ��s�̨ΤƨD�ѡC |
�ҡG
�[�J 2X1 + 3 X2 <=24
Table 6.22
|
|
BasicVar. |
Eq. |
Coefficient of: |
r.h.s. |
||||||
|
Z |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
||||
|
Revised final tableau |
Z |
(0) |
1 |
9/2 |
0 |
0 |
0 |
5/2 |
0 |
45 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
3/2 |
1 |
0 |
0 |
1/2 |
0 |
9 |
|
|
x4 |
(3) |
0 |
-3 |
0 |
0 |
1 |
-1 |
0 |
6 |
|
|
x6 |
New |
0 |
2 |
3 |
0 |
0 |
0 |
1 |
24 |
|
�W�����ذϬ����A���AEq(2) x (�V3) + New Eq. �i�ﵽ�A���G�p�U���G
|
Converted to proper form |
Z |
(0) |
1 |
9/2 |
0 |
0 |
0 |
5/2 |
0 |
45 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
3/2 |
1 |
0 |
0 |
1/2 |
0 |
9 |
|
|
x4 |
(3) |
0 |
-3 |
0 |
0 |
1 |
-1 |
0 |
6 |
|
|
x6 |
New |
0 |
-5/2 |
0 |
0 |
0 |
-3/2 |
1 |
-3 |
x6���t�ơA�ҥH (0,9) ���Ѭ� non-feasible, ���]�� Row 0 ���Y�Ƨ����D�t�A�ҥH�� Superoptimal, �i�A�z�L Dual Simplex Method �D�Ѩño�X�U���G
|
Reoptimzation after one iteration of Dual simplex Method |
Z |
(0) |
1 |
1/3 |
0 |
0 |
0 |
0 |
5/3 |
40 |
|
x3 |
(1) |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
|
|
x2 |
(2) |
0 |
2/3 |
1 |
0 |
0 |
0 |
1/3 |
8 |
|
|
x4 |
(3) |
0 |
-4/3 |
0 |
0 |
1 |
0 |
-2/3 |
8 |
|
|
x5 |
New |
0 |
-5/3 |
0 |
0 |
0 |
1 |
-2/3 |
2 |
(0, 8) ���s���̨θѡA�BZ = 40 ���s�� O.F.V.
���t�Ϊ��ӷP�פ��R�аѼƳW��
���]�Q�A�Ѥ@�өΦh���ܼƦb�Y�@�϶����s���ܰʮɡA���̨θѤ��ܰ�
�v�T�p��A���ɥi�İѼƳW���覡�i��C
���]�ĤG����� rhs �� b2 ���Ȧb 12 �P 24 ���s���ܰʡA
�h�N b2 �w�q�� 12 + �c�A�䤤 �c = 0 �� 12
�H ²��k�i��D�ѡA�i�o�X�H�U�������G�G
�� = 36 + 3/2 * �c
��1 = 2 - 1/3 * �c
��2 = 6 + 1/2 * �c
��3 = 2 + 1/3 * �c
��4 = 0
��5 = 0
���k�P�ɾA�Ω� O.F.V. �έ�����Y�ܼƤ��Y�ơC
��i�P�ɤ��R�ƭ��ܼƤ��Y�Ƥ��ܰʩμƭӭ���� rhs �Ȥ��ܰʡC
�@�~
1. �ХH����ĭz�u�ʳW�������D�а��D�]Primal-Dual�^���Y�����z�ﰸ�ʡA�j�ﰸ�ʡA���ɩʡA�ι�٩ʡC
2. �ХH����ĭz�u�ʳW�����u��̨ΤƤ��R�v�A�]�A�G
�@�몺�ӷP�פ��R�Gƫ O.F.V. �� �Y�ܼƫY�Ƨ���
Ƭ �Y�@����� �Y�ܼƫY�Ƨ���
ƭ �Y�@����� rhs ���ȧ���
�ΰѼƳW��