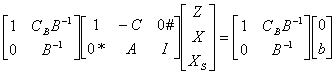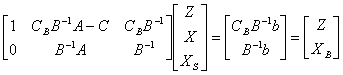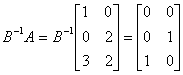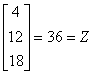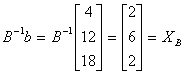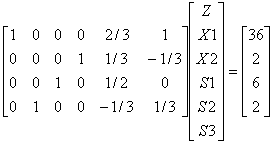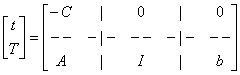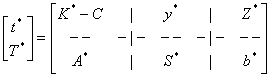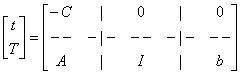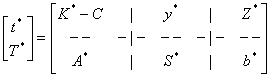Chap. 5 ²��k���z��
5.1�����W��
Constraint boundary equation: �������ɤ�{��
�H�������N��������������ҧΦ�����{���C
Ai1 X1 + Ai2 X2 + .... + Ain Xn = bi, i = 1,2,...,m
���ؤ�{���w�q�Fn �תŶ����X��ϧΡC
|
n |
�W��(HyperPlane) |
|
2 |
�u |
|
3 |
�� |
|
Max Z = 3 X1 + 5 X2 |
|
|
s.t. |
|
|
|
X1 <= 4 2X2 <=12 3X1 + 2 X2 <=18 X1>=0, X2>=0 |
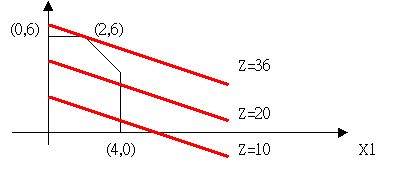
�̤W�ҡA#
of functional constraints = m =3
# of non-negativity = n=2, # of decision variables = n = 3
|
�i��� Feasible Solution |
�����Ҧ�������@�ոѡC |
|
�i��� Feasible Domain |
�Ҧ��i��ѩҧΦ������X�C |
|
��� Boundary |
�����@�өΦh����ɤ�{�����i��Ѻ٤����i��줧��ɡC |
|
���I Corner Point |
�b n �תŶ��� m+n �� Boundary Eq.�إ��� n���p�ߩҨD�o���Ѻ٤��C |
���a�Dzߥ� Excel ���p�ߦ��A�ФU�� Excel6.zip
|
���I�i��� Corner Point Feasible Solution |
�Ѩ��I�ޥӪ��w�q�G�ëD�Ҧ����I�Ҭ��i��ѡA�u���b�i��쪺��ɤW�����I�~�O���I�i��ѡC ���i����ޥӪ��w�q�G��������i�s����L��ӥi��Ѫ��u�q�W���i��ѡC A feasible
solution that does not lie on any line segment connecting two other feasible
solutions. |
|
�۾F���I�i��� Adjacent Corner Point Feasible Solution |
�Y�⨤�I�Q�٬��۾F�A�h�s���ӤG�I��'�u'�������i��줧��ɡC�G�۾F���I�����u���@��ɤ�{�����P |
|
�w�q��{�� Defining
Equation |
�M�wCP
����ɤ�{���C Refer
to p.156 Table 5.1
and Table
5.2 |
�q�h1a�G
|
�Y Optimum Solution �u���@�աA�h�������I�i��ѡC |
�q�h1b�G
|
�Y Optimum Solution ���h�աA�h�䤤�ܤ֦��G�լ��۾F���I�i��ѡC |
�ҩ��Gsee p.159 of Text Book
���]�s�b�@�ӳ��u�ѡA�B��D���I�i��ѡC
�Ѩ��I�i��Ѫ��w�q�i���䬰�u��������i�s����L��ӥi��Ѫ��u�q�W���i��ѡv�C
�Y�D�����I�i��ѡA�h��i������i�s����L��ӥi��Ѫ��u�q�W�C

�p�W�ҭz�AZ*�Y�D����Z1�B����Z2 �A�hZ* ���i�ର���u�ѡC
�q�h2�G
|
���I�i��Ѥ��ƥئ����C |
�ҩ��Gsee p.160 of Text Book
���]�b n �תŶ������D���� m+n �ӭ���A�h�� m+n ����ɤ�{���C
|
���� n �Ӥ�{���p�ߨD�ѡC |
�̦h�i�� |
|
|
���I���ƥءANcp |
Ncp < |
8 < 10 |
|
���I�i��Ѥ��ƥءANcpfs |
Ncpfs < Ncp |
5 < 8 |
�q�h3�G
|
�@���I�i��ѭY�u��Ҧ����۾F���I�i��ѡA�h���u���L���I�i��ѡC �]�Y���X�^ |
m = 50�A n = 50�A![]() =
=![]() =
=![]() �ո�
�ո�
�H²��k�h�ѡA�u���D�� 100 �Ө��I�i��ѡC
�ҩ��Gsee p.161 of Text Book
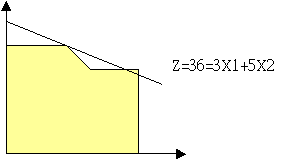
Fig.5.3
�[�JSlack variables (�X�i)���᪺�����w�q�G
|
Augmented CP solutions�X�i���I��= basic solutions��� |
�[�JSlack
variables and/or Artificial variables ���᪺���I�� |
|
|
��ѡG�]�Am�Ӱ��ܼơA��l���D���ܼƤ��Ȭ�0�Am���\�୭����Ӽ� |
||
|
�����ܼ� Indicating
variable |
�i�N���Y�@��ɤ�{�����ܼơC Refer
to p.162 Table 5.3
and p.164 Table 5.4 |
|
|
Augmented CPF solutions �X�i���I�i���� = Basic Feasible solutions�i��� |
�[�JSlack variables and/or Artificial variables ���᪺���I�i��� |
|
�i��ѡG�O�Ҧ���m�����ܼƳ�
>=0 ���@�հ�ѡA�Y���@���ܼƤ��Ȭ�0�A���i��ѳQ�٬��h�� (degenerate)�C |
|
Table 5.5 BF solutions for the Wyndor Glass Co. Problem (p.164)
Table 5 .6 Basic infeasible solutions for
the Wyndor Glass Co. Problem (p.164)
Table
5.7 Sequence obtained by the Simplex method for the Wyndor Glass Co. Problem
|
Iteration |
CPF solution ���I�i��� |
Defining Eq. �w�q��{�� |
Nonbasic Var. �D���ܼ� |
|
0 |
(0,0) |
X1=0 X2=0 |
X1=0, X2=0 |
|
1 |
(0,6) |
X1=0 2X2=12 |
X1=0, X4=0 |
|
2 |
(2,6) |
2X2=12 3X1+2X2=18 |
X4=0, X5=0 |
5.2 �ץ�²��k
�x�}����
|
�@��Ҧ� Max: Z = 3 X1 + 5 X2 |
s.t. X1 <= 4 2 X2 <= 12 3 X1 + 2 X2 <= 18 X1 >= 0 X2 >= 0 |
|
�q�� |
�x�}���ܪk |
|
Max: Z =C1 X1 + C2 X2 + ..+Cn Xn s.t.
i = 1, 2, ..., m Xj >= 0, j = 1, 2, ..., n |
Z = C X A X <= b X >= 0 �䤤�AC = [ C1, C2, C3, ... , Cn ]
|
�W�Ҧ�n ���ܼơAn �תŶ��An + m �ӭ���A�ݭn m �� slack variables�A
�[�W m�� slack variables ���᪺�Ҧ��p�U�ҥܡG
|
�@��Ҧ� Max Z Z-3X1-5X2+0S1+ 0S2+0S3 = 0 s.t. X1 + 1 S1+ 0 S2+ 0 S3 = 4 2 X2+ 0 S1+ 1 S2+ 0 S3 = 12 3 X1+2 X2+ 0 S1+ 0 S2+ 1 S3 = 18 |
�x�}���ܪk �� = [ C, 0 ] s.t. [A, I] �䤤 |
|
|
|
|
��� [ A, I ] �D�ѡG ��B= ��-1 * b �w�q ��B= [C, 0] ���h���D���ܼƤ��������A�A���s�ƦC�H�t�X��B ������ �� = ��B ��B = ��B�]��-1 * b �^ |
|
�d�ҡG
|
Max: Z = 3 X1 + 5 X2 |
Max: Z = [3, 5] |
|
s.t. X1 <= 4 2 X2 <= 12 3 X1 + 2 X2 <= 18 X1 >= 0 X2 >= 0 |
s.t.
A X <= B X = |
�[�W slack variables ����
|
Max Z Z - 3 X1 - 5 X2 + 0 S1 + 0 S2 + 0 S3 = 0 s.t. X1 + S1 = 4 2 X2 + S2 + = 12 3 X1 + 2 X2 + S3 = 18 |
|
�x�}���ܪk |
|
|
�H�x�}����²��k�D��
|
iter 0 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
��}B = ��[ A,I ] �h���D���ܼƤ������� = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
��B = ��[ C, 0 ] �h���D���ܼƤ������� = [ 0 0 0 ] |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
��B =��-1 b
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Z = CB��B = [0 0 0] |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
iter 1 |
X2 �i�J�A S2 ���} |
||||||||||||||||||||||||||||||||||||||||||
|
��B = |
B = |
��B = [ 0 5 0 ] |
|||||||||||||||||||||||||||||||||||||||||
|
(a) ��-1= |
(b) ��-1�� = ��-1 |
||||||||||||||||||||||||||||||||||||||||||
|
(c) ��B ��-1 = [ 0 5 0] |
|||||||||||||||||||||||||||||||||||||||||||
|
(d) ��B ��-1�� -�� = [0 5/2 0] |
|||||||||||||||||||||||||||||||||||||||||||
|
(e) ��B= ��-1 b = ��-1 |
|||||||||||||||||||||||||||||||||||||||||||
|
(f) �� =��B ��B = [ 0 5 0 ] |
|||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
iter 2 |
X1 �i�J�AS3 ���}�� |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
��B = [0 5 3] |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
�ץ��x�}����²��k
|
||||||||||||||||||||||||||||||||||||||||
|
�x�}���� (iteration 0) |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
0* �� I �� dimension (m x m) �ӨM�w�䬰 m x 1 �� �s�x�}�A 0# �� I �� dimension (m x m) �ӨM�w�䬰 1 x m �� �s�x�}�A C �� 1 x n ���x�}�A A �� m x n ���x�}�C |
|
��(1)����P��
|
���H�W�Ұ������Aiter. 0 �� 1 ���A�ȥH iter. 2 ���ܽd�C
|
�ѫe�Ҥw�� �Яx�} = |
(a) |
||||
|
(b) |
(c) ��B��-1 = [0 5 3] ��-1 = [0 3/2 1] |
||||
|
(d) ��B��-1�� - �� = [ 0 3/2 1 ] = [0 0] |
(e) ��B��-1 b = [ 0 3/2 1 ] |
||||
|
(f) |
|
||||
|
|
|||||
|
�̫ᤧ�̨δ���: row 0 ( O.F.) ���D���ܼƤ��Y�ƵL�t�ƫh��Ѭ��̨θѡC |
|
||||
���a�DzߥH Excel ���x�}���B��A�ФU�� Excel6.zip
5.3 ²��k�����[
���]���Y�@ LP �Ҧ��p���D�ҥܡA��g�L�X���� iteration����A�̲ױo��U��k���ҥܤ��̲ѡC�b���D�P�̲Ѥ����s�b�ۤ@�����Y�A���`�Y�b�����������[���S���N�q�C
|
���D |
�̲� |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
�䤤
|
��* =��B��-1 A = y*A |
��* =��-1 A |
��* =��-1 |
|
b* =��-1 b |
y* =��B��-1 |
��*=��B��-1 b = y* b |
�i�[��X�H�U������Y���G
|
��*= t + y* T = [ -C 0 0 ] + [y*A y*I y*b] = [y*A-C y*I y*b] |
|
��*= ��*T = ��-1 T = [��-1A ��-1I ��-1b] |
���סG�u�n�D�o y* �P ��* �A�Y�i��![]() �D�X
�D�X ![]()
|
|
�b��l�x�}���� row j * |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�d�ҡG |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
�d�ҡG
|
��l�x�} |
�̲ׯx�} |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
����
|
row 1: ��l�x�} (row 1)*1 + (row 2)*1/3 + (row 3)*(-1/3) |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
row 2: ��l�x�} (row 1)*0 +(row 2)*1/2 +(row 3)*0 |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
row 3: ��l�x�} (row 1)*0 + (row 2)*(-1/3) + (row 3)*(1/3) |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
�i�@�B�[����D�P�̲Ѥ��C ��(�Y O.F.)
|
|
|
|
[t] = [-C 0 0] |
[t*] = [K*-C y* Z*] = [ y*A-C y* y*b] |
²��k���믫�Y�b��M�@�հ��ܼƤΨ�۹������i��ѡA�ϱo�C�����Y�ƬҬ��D�t��ơC�]max problem�^
|
��*= y*�� |
�w�w�w>>>>�w�w�w�w |
��o = y�� |
|
s.t. y*�� - C >= 0 y* >= 0 |
�h�� *�A�� �� �� ��o �`�ƶ����� rhs �w�w�w>>>>�w�w�w�w |
s.t. y�� >= C y >= 0 |
|
|
�������D���D���Y���Ѩ� |
|


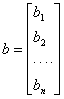
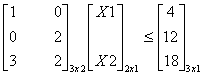

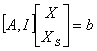



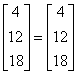
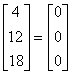

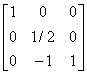
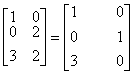
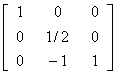
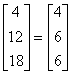
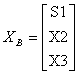
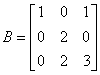
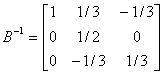
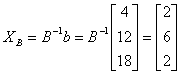
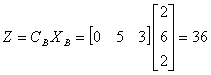
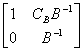 �i�ɥX�U��
�i�ɥX�U��