Chap.4 求解線性規劃問題-簡算法
OPTIMIZATION with
<= constraints
OPTIMIZATION with
>= constraints
OPTIMIZATION with
= constraints
OPTIMIZATION with
>=，<=，＝ constraints
4.5 Tie breaking
in the Simplex method
4.7 Post-Optimality Analysis 事後最佳化分析
LP Solutions 之分析
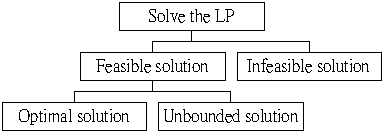
正常的 LP 模式，其求解過程應循上圖之最左路線。
簡算法的本質
Algorithm
(演算法)
角點可行解的性質：
若最優解洽為一個，必為角點可行解。
若有多個最優解，其中至少有兩個解是相鄰的角點可行解。
角點可行解的個數有限。
某角點可行解若比其全部相鄰的角點可行解為優，其即為最優解。
4.2 簡算法的建立
標準型：Maximization with <=
constraints
|
Maximize:
Y = 50 Hc + 75 Hs s.t. Hc + Hs <= 240
120 Hc + 40 Hs <= 19200 5 Hc + 10 Hs <= 2000 Hc, Hs
>= 0 |
本題為 3 x 2 (or m x n) 之 LP，有三個限制式，加上
slack variables 之後應有五個變數 (m=3, n=2, n'= m + n =5) 個變數，其中 2 (or n) 個變數應一直維持為 0，稱之為「非基變數」(non-basic
variables)；且，另外的 3 (or m) 個變數應一直維持為≠ 0，此 3 (or m) 個 ≠ 0之變數稱之為「基變數」(basic
variables)，其組合稱之為「基底」 (basis)或稱可行基解。
|
名詞 |
說明 |
|
Augmented solution (擴張解) |
原題中的不等式透過差額變數的加入而將問題改為等式形式的解。 原可行域內之任一組解現在稱為擴張解。 如(3,2) -> (3,2,1,8,5) |
|
Basic solution (基解) |
擴張的角點解。基解不一定就是可行解。如(4,6) ->
(4,6,0,0,-6) |
|
Feasible basic solution (可行基解，基底) |
擴張的角點可行解。由基變數與非基變數組成。 |
|
basic variables (基變數) |
=限制式的個數，上例的基變數個數=3 = m |
|
degree of freedom (自由度) |
其值 = n - m |
|
Non-basic variables (非基變數) |
非基變數個數 = 方程組的自由度，上例的非基變數個數 = 2非基變數之值
= 0 |
4.3 代數型簡算法
參見The demonstration of OR Courseware Algebraic
Form
4.4 表列型簡算法
參見The demonstration of OR Courseware Tabular
Form
OPTIMIZATION with <= constraints
OPTIMIZATION （最佳化）：可以是極大化，亦可以是極小化
|
Maximize:
Y = 50 Hc + 75 Hs s.t. Hc + Hs <= 240
120 Hc + 40 Hs <= 19200 5 Hc + 10 Hs <= 2000 Hc, Hs
>= 0 |
簡算法求解步驟：
使用非負的鬆弛(差額)變數 (SLACK variables)，將不等式改為等式 (Si >= 0).
|
Hc + |
Hs + |
S1 |
|
|
=
240 |
|
120 Hc + |
40 Hs + |
|
S2 |
|
=
19200 |
|
5 Hc + |
10 Hs + |
|
|
S3 |
=
2000 |
三個限制式，五個變數 (m=3, n=5)
First step：
Transformation of the O.F.: move all items to lhs
Y - 50 Hc - 75 Hs = 0
Start Simplex Method：
Find the programmed variable（*）樞欄and controlling constraint（**）樞列. 二者之交點稱為
PIVOT pt. or Augmenting Element. 樞數
在 base line 中選擇 programmed
variable(*)之規則：找出影響力最大的系統參數，即選擇移動的方向。
For Maximum problem, use the largest negative.
For Minimum problem, use the largest positive.
在 1st Column（第一行）中選擇 controlling
constraint (**) 之規則：
找出系統參數（*）在那一個限制式（**）上之可行解為最小。即選擇移動到哪裡停止。假設 C = B/A，將 C 之值填入第一行 (Col.1)，再找最小的正數.
Tableau 1:
O.F. 係數之所在列，稱之為 Base Line 啟始的可行基解為 (0, 0,
240,19200,2000) Hs 進入「基底」， S3 離開「基底」 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Elementary Transformation:
Make the coefficient of the Programmed variable of
controlling constraint to 1 (將樞列之係數除以樞數)
Make the coefficient of the same variable in other
constraints to 0.
|
If there are still negative values in
base line, return to step 3.
Tableau 2:
Hc 進入「基底」， S1 離開「基底」 |
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
判斷：在 base line 找不到負數，大功告成 解答：Hc =
80, Hs = 160, S1 = 0, S2 = 3200, S3 = 0 Objective Function Value (O.F.V.) = 16000 |
||||||||||||||||||||||||||||||||||||||||
|
FACTs: 2 unknowns, 2 limiting factors, Constraint 2 is not a limiting factor
in this example. 觀念 :
其中，m: number of constraints, n: number of unknowns. |
|
Max: Y = 6 X1 + 4 X2 s.t. 2 X1 + 3 X2 <= 100 4 X1 + 2 X2 <= 120 X1, X2 >= 0 |
Max:
Y - 6 X1 - 4 X2 + 0 S1 + 0 S2 = 0 s.t. 2 X1 + 3 X2 + S1 = 100 4 X1 + 2 X2 + S2 = 120 Xi, Si
>= 0 |
|
|
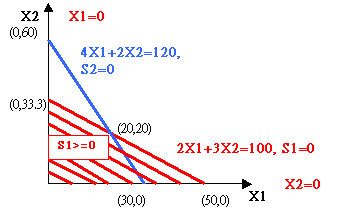
由 (0,0)沿X1出發，此時S1, S2 均不等於0 |
|
||||||||||||||||||||||||||||
|
|
X1 entering, S2 leaving，代表 X1不等於0，進入S2=0 的邊界
抵達 (30,0)準備朝S2=0 的邊界上移動，此時S1與X1為不等於0，X2與S2為0 |
|
||||||||||||||||||||||||||||
|
|
X2 Entering, S1 Leaving，代表 X2不等於0，進入S1=0 的邊界
|
|
||||||||||||||||||||||||||||
|
|
抵達 (20,20)，準備朝 S1=0 的邊界上移動，移動前先測試是否已為最佳解，
在 base line 找不到負數，已為最佳解，所以X1 = X2 = 20, O.F.V. = 200 |
|
請自行練習書上範例 p.87
OPTIMIZATION with >= constraints
Minimize Y = 8 Xa + 4 Xb + 3 Xc
s.t.
30 Xa + 20 Xb + 10 Xc
>= 120
7 Xa + 2 Xb + 6 Xc >= 42
Xa, Xb, Xc
>= 0
step 1: 使用 Slack Variables (S1, S2 >= 0)
30 Xa + 20 Xb + 10 Xc - S1 = 120
7 Xa + 2 Xb + 6
Xc - S2
= 42
但是，如此一來，便無法由 Xa = Xb = Xc = 0 開始，
解決之道：使用人工變數 (Artificial
Variables)。
step 2: 使用 人工變數
30 Xa + 20 Xb + 10 Xc - S1 + A1 = 120 [1]
7 Xa + 2 Xb + 6
Xc -
S2 + A2
= 42 [2]
由 Xa = Xb = Xc = S1 = S2 = 0 開始求解
step 3: 修改目標函數，加入 PENALTY為了使所用的人工變數在最後會消失。
在人工變數之係數使用 Penalty (原義為處罰)，如下所示：
MINimize Y = 8 Xa + 4 Xb + 3 Xc + P A1 + P A2
注意：本例若為求極大，則「目標函數」應修正如下：
MAXimize Y = 8 Xa + 4 Xb + 3 Xc - P A1 - P A2
Penalty 為一極大之數，其目的在使人工變數在求解過程中即自動趨近 0。在教科書中以M為極大數，並稱為大M法 (Big
M Method)，此名詞只為方便說明，並非通用之說法。
step 4: 修改目標函數，除去人工變數
由 step 2 中之 [1], [2] 可導出 A1, A2 如下：
A1 = 120 - 30 Xa - 20 Xb - 10 Xc +
S1
A2 = 42 - 7 Xa
- 2 Xb - 6 Xc + S2
將之代入「目標函數」，可將 A1, A2 刪除不用。
step 5: 重新整理目標函數之各項係數
Y = 8 Xa + 4 Xb + 3 Xc + P (..) + P (..)
=
(8 - 37 P) Xa + (4 - 22 P) Xb + (3 - 16 P) Xc + P S1 + P S2 + 162 P
─> Y + (37 P - 8) Xa + (22 P - 4) Xb
+ (16 P - 3) Xc - P S1 - P S2 = 162 P
step 6:
以正規解法求解
|
Col.1 |
=0 |
=0 |
=0 |
=0 |
=0 |
|
|
|
|
|
Xa |
Xb |
Xc |
S1 |
S2 |
A1 |
A2 |
rhs |
|
4 |
30 |
20 |
10 |
-1 |
|
1 |
|
120 |
|
6 |
7 |
2 |
6 |
|
-1 |
|
1 |
42 |
|
|
37P-8 |
22P-4 |
16P-3 |
-P |
-P |
|
|
162P |
在 base line 中選擇 programmed
variable(找影響力最大的系統參數)
For Max. problem, use the largest
negative.
For Min. problem, use the largest
positive
Only Artificial Variables to be nonzero
at first, find the largest positive in base line, Find the smallest positive
value in first column.
PIVOT element found --> Xa ≠ 0,
then A1 = 0
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
PIVOT element found --> Xc ≠
0, then A2 = 0 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
PIVOT element found --> Xb ≠
0, then Xa = 0 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
在 base line 找不到正數，大功告成 Xa = 0, Xb = 3, Xc = 6， Minimum value = 30 |
|
觀念： 3 unknowns, 2 constraints -> one of the unknowns must be
zero
OPTIMIZATION with = constraints
For equality constraint, an artificial variable
(A) must be added to the constraint and a term P * A must be either added to
(minimization problem) or subtracted from (maximization problem) the objective
function. P.104 of Text
Book.
範例:
OPTIMIZE Y = .....
s.t.
2 Xa + 3 Xc = 16
can't start from Xa = Xc = 0，need an
artificial variable。
其它作法同前一節之敘述，需在O.F. 中加入 Penalty。
OPTIMIZATION with >=，<=，＝ constraints
範例：
Minimize Y* = -6 X1 - 4 X2
s.t.
2 X1 + 3 X2 <= 30
3 X1 + 2 X2 <= 24
X1 + X2 >=
3
X1 , X2 >=
0
|
Max. Y = 6 X1 + |
4 X2 |
|
|
|
|
|
|
Max. Y = 6 X1 + |
4 X2 |
|
|
|
- T A1 |
|
|
s.t. |
|
|
|
|
|
|
|
2 X1 + |
3 X2 + |
S1 |
|
|
|
= 30 |
|
3 X1 + |
2 X2 + |
|
S2 |
|
|
= 24 |
|
X1
+ |
X2 |
|
|
- S3 |
+ A1 |
= 3
……. [1] |
|
O.F.:Y - 6 X1 - |
4 X2 |
|
|
|
+ T A1 |
= 0 ……. [2] |
|
式 [1] * (-T) + 式 [2] 可除去O.F.中的人工變數
A1，得下式： |
||||||
|
O.F.:Y- (T+6) X1 |
-(T+4) X2 |
|
|
+ T S3 |
|
= -3 T |
求解：
|
Col.1 |
X1 |
X2 |
S1 |
S2 |
S3 |
A1 |
rhs |
|
15 |
2 |
3 |
1 |
0 |
0 |
0 |
30 |
|
8 |
3 |
2 |
0 |
1 |
0 |
0 |
24 |
|
3 |
1 |
1 |
0 |
0 |
-1 |
1 |
3 |
|
|
-(T+6) |
-(T+4) |
|
T |
|
|
-3T |
|
Col.1 |
X1 |
X2 |
S1 |
S2 |
S3 |
A1 |
rhs |
|
|
0 |
1 |
1 |
0 |
2 |
-2 |
24 |
|
|
0 |
-1 |
0 |
1 |
3 |
-3 |
15 |
|
|
1 |
1 |
0 |
0 |
-1 |
1 |
3 |
|
|
0 |
2 |
|
|
-6 |
|
18 |
|
Col.1 |
X1 |
X2 |
S1 |
S2 |
S3 |
A1 |
rhs |
|
12 |
0 |
1 |
1 |
0 |
2 |
-2 |
24 |
|
5 |
0 |
-1/3 |
0 |
1/3 |
1 |
-1 |
5 |
|
-3 |
1 |
1 |
0 |
0 |
-1 |
1 |
3 |
|
|
0 |
2 |
0 |
0 |
-6 |
|
18 |
|
Col.1 |
X1 |
X2 |
S1 |
S2 |
S3 |
A1 |
rhs |
|
|
0 |
5/3 |
1 |
-2/3 |
0 |
0 |
14 |
|
-5 |
0 |
-1/3 |
0 |
1/3 |
1 |
-1 |
5 |
|
|
1 |
2/3 |
0 |
1/3 |
0 |
0 |
8 |
|
|
0 |
0 |
0 |
2 |
0 |
-6 |
48 |
Col.1的計算值不存在正數
，結束iteration。
Ymax=48, --> Y*min= -48
SUMMARY
Add SLACK Variables (Si) to <=
constraint
Substract SLACK variables (Si) from
>= constraints (sometimes use term 'surplus' instead of 'slack')
Add ARTIFICIAL variables (Ai) to >=
or = constraints then,
Add (minimization problem) or substract
(maximization problem) "P * Ai" in the Objective Function (O.F.).
Eliminate all Ai from O.F. by
substitution.
Move all non-constant terms to lhs in
O.F.
Use 簡算法的 solution procedures to solve.
在 base line 中選擇 programmed
variable (*)之規則：
Maximization problem：找絕對值為最大之負數
Minimization problem：找絕對值為最大之正數
在 1st Column中選擇
controlling constraint (**) 之規則：找「最小的非負數」
大功告成之判斷規則：
Maximization problem：在 base line 中找不到負數時
Minimization problem：在 base line 中找不到正數時
4.5 Tie breaking in the Simplex method
Tie for the
entering basic variable 入基變數相等時，可任意選擇
Tie for the
leaving basic variable出基變數相等時，屬退化模式
No leaving basic
variable 無出基變數，Z值無上限
Multiple Optimal Solutions 在找到一個最佳解之後Z值便不會改變
4.6 其它 LP 模式
無解之 LP model (Infeasible LP's) p.119 of Text Book
MAX: X1 -
X2
s.t. 4 X1 - 2 X2 <=
8
3 X1 + 9 X2 <= 21
X2 >= 3
X1 >= 0
無限多組解之 LP model
(Unbounded LP's)
MAX: X1 + 2 X2 + X3
s.t. 2 X1 + X2
+ X3 <= 20
X1 + 3 X2 + 3 X3 <= 30
X1, X2, X3 >= 0
求最小化的 LP Model p.111 of Text Book
MIN: Z = X1 + 2 X2 + X3
等於 MAX: Z* = (- Z) = -X1 -2 X2 - X3
解出Z*
後，記得正確答案應該是 Z = -Z*。
限制式的rhs 為負數 p.107
of Text Book
-3X1 - 2
X2 <= -18
相當於 3X1 + 2 X2 >= 18
使用 Surplus 變數與人工變數求解。
變數必須為負數時 p.120 of Text Book
1.
有界的負變數：當變數不是>=0 而是 >=某負數 (Lj) 時
使用變換變數的方式先調整變數再以Simplex 法求解：
Xj' = Xj
-Lj, 故 Xj' >= 0
2.
無界的負變數：
Xj若無下界，則用兩個新的非負變數之差來替代該變數，簡介如下：
Xj
= Xj+ - Xj-
其中，Xj+ 與
Xj- >=0。但若所有變數皆需如此處理，則此法會使變數數目加倍。較好的做法是：
Xj
= Xj' - Xj''
-Xj''為所有負變數中的最小值，Xj' 與
Xj'' >=0，如此處理則元模式只會增加一個變數。
4.7 Post-Optimality Analysis 事後最佳化分析
Shadow Price影價yi*：簡算表中最末表格中baseline 中差額變數的係數值。
Refer to Table 4.8 @ p.99 of
TextBook
|
Iteration 0 |
Basic V. |
Z |
X1 |
X2 |
X3 |
X4 |
X5 |
Rhs |
|
|
Z |
1 |
-3 |
-5 |
0 |
0 |
0 |
0 |
|
|
X3 |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
|
|
X4 |
0 |
0 |
2 |
0 |
1 |
0 |
12 |
|
|
X5 |
0 |
3 |
2 |
0 |
0 |
1 |
18 |
|
Iteration 2 |
Basic V. |
Z |
X1 |
X2 |
X3 |
X4 |
X5 |
Rhs |
|
|
Z |
1 |
0 |
0 |
0 |
3/2 |
1 |
36 |
|
|
X3 |
0 |
0 |
0 |
1 |
1/3 |
-1/3 |
2 |
|
|
X2 |
0 |
0 |
1 |
0 |
1/2 |
0 |
6 |
|
|
X1 |
0 |
1 |
0 |
0 |
-1/3 |
1/3 |
2 |
|
原：Z= 3 X1+ 5 X2+ 0 X3+ 0 X4+
0 X5 |
終：Z= 0 X1+ 0 X2+ 0 X3- 3/2
X4- 1 X5 |
|
X1 = 4 - X3 |
差額變數X3, X4, X5 各加1(相當於差額變數值不變但三限制式之rhs各少1)，可使Z減少相對應的量 (與原Z值相比較)。 |
|
2X2=12-X4 |
差額變數X3, X4, X5 各少1(相當於差額變數值不變但三限制式之rhs各加1)，可使 Z增加相對應的量 (與原Z值相比較)。 |
|
3X1+2X2=18-X5 |
Shadow Price(影價)又稱 Dual Price |
***參考 LP-ShadowPrice.htm ，下載 LP-shadowPrice.xls
***參考補充資料 What is Reduced Cost ?
資源i 的影價可用來計算該資源的邊際價值(marginal value)
邊際價值：增加資源 (bi) 可使Z增加的比率
敏感度分析 (Sensitivity Analysis)：在原始模式中一次改變一個參數以檢查該參數對最優解的影響。
參數線性規劃(Parametric Linear
Programming)：簡稱參數規劃，在原始模式中有系統的探討多個參數同時改變時對最優解的影響。
