Chap 11. Game Theory 博奕理論
第一種情況：有凌越策略 (dominated strategies)
第二種情況：無凌越策略、有鞍點 (Saddle point)
博奕理論探討面對競爭問題之決策過程，一對一的競爭以局論或對局(two person game)稱之，有大於兩個以上的競爭者則以競局(n person game)稱之。本章以討論對局為主。
11.1 對局之公式化
Two person
zero-sum game 零和對局：兩個players, 甲輸的即為乙贏的。
對局之特徵：玩者甲的策略、玩者乙的策略、報酬表。
對局開始之前，前述三者均為公開，玩時，雙方各選一策略，但不知對方將選擇何種策略。
What is 策略
(Strategy): a predetermined rule that specifies completely how one intends to
respond to each possible circumstance at each stage of the game.
報酬表 (payoff
table) 通常只列出玩者甲的報酬。
玩者甲與玩者乙均為有理性(rational)且雙方所選的策略均只想提高自己的報酬。
Chapter 20 探討「決策分析」與對局相通，只是其中的一個玩者為Nature，其策略的選擇係依據自然發生的機率。
11.2 範例
最末兩天行程安排的競選策略：
第一策略：City A, B 各一天
第二策略：City A兩天
第三策略：City B兩天
事實上，在第一天開始後雙方的初步動向已知，可刪除上述的一個策略，重新訂新的對策。
Table 11.2. Form of the Payoff Table
|
|
甲之淨贏總票數 (單位：千票) |
||
|
Strategy |
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
甲之第一策略 |
|
|
|
|
甲之第二策略 |
|
|
|
|
甲之第三策略 |
|
|
|
第一種情況：有凌越策略 (dominated strategies)
(p.474 of Textbook)
Table 11.2. Form of the Payoff Table
|
|
甲之淨贏總票數 (單位：千票) |
||
|
Strategy |
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
甲之第一策略 |
1 |
2 |
4 |
|
甲之第二策略 |
1 |
0 |
5 |
|
甲之第三策略 |
0 |
1 |
-1 |
就乙方言，沒有凌越策略，就甲方言，第三策略永遠不如第一策略，所以可將第三策略予以刪除。
|
Strategy |
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
甲之第一策略 |
1 |
2 |
4 |
|
甲之第二策略 |
1 |
0 |
5 |
由上表可看出乙之第三策略永遠不如乙之第一與第二策略，所以第三策略可予以刪除。
|
Strategy |
乙之第一策略 |
乙之第二策略 |
|
甲之第一策略 |
1 |
2 |
|
甲之第二策略 |
1 |
0 |
由上表可看出甲之第二策略永遠不如甲之第一策略，所以第二策略可予以刪除。
|
Strategy |
乙之第一策略 |
乙之第二策略 |
|
甲之第一策略 |
1 |
2 |
由上表可看出乙之第二策略永遠不如乙之第一策略，所以第二策略可予以刪除。
|
Strategy |
乙之第一策略 |
|
甲之第一策略 |
1 |
由此結果可知雙方均選第一策略，且對局之值 (Value of the game)為1代表甲將贏乙1000張票。當對局之值為0時代表該局為和局(fair game)。
凌越的觀念可擴展到一特定列(或行)被其他所有列(或行)之凸性組合所凌越的情況。以下例說明：
例一、假設在 3 x 2 Game 中，其Payoff table 如下：
|
列一 |
2 |
4 |
|
列二 |
5 |
1 |
|
列三 |
3 |
2 |
因為1/3 (列一) + 2/3 (列二) = 1/3 [2 4]+ 2/3 [5 1] = [4 2] >= (列三)
所以列三可予以刪除。
例二、假設在 2 x 3 Game 中，其Payoff table 如下：
|
行一 |
行二 |
行三 |
|
1 |
6 |
3 |
|
6 |
2 |
5 |
因為3/4 (行一) + 1/4 (行二) = 3/4 [1 6]T+ 1/4 [6 2] T = [9/4 5] T <= [3 5] T
所以行三可予以刪除。
第二種情況：無凌越策略、有鞍點 (Saddle point)
(p.475 of Textbook)
|
Strategy |
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
列最小值 |
|
甲之第一策略 |
-3 |
-2 |
6 |
-3 |
|
甲之第二策略 |
2 |
0 |
2 |
0 *** |
|
甲之第三策略 |
5 |
-2 |
-4 |
-4 |
|
欄最大值 |
5 |
0*** |
6 |
|
甲採小中取大策略：想極大化其最小收益，小中取大值(Maximin value)為對局之值的下限。
乙採大中取小策略：想極小化其最大損失，大中取小值(Minimax value)為對局之值的上限。
當對局之下限 =對局之上限 (
)，此項既為所屬之列中的最小者，亦為所屬之欄中的最大者，稱為鞍點。
若有鞍點，雙方不能利用對方的策略以增進己方的優勢，所以此解為穩定解。
第三種情況：無凌越策略、無鞍點
|
Strategy |
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
列最小值 |
|
甲之第一策略 |
0 |
-2 |
2 |
-2*** |
|
甲之第二策略 |
5 |
4 |
-3 |
-3 |
|
甲之第三策略 |
2 |
3 |
-4 |
-4 |
|
欄最大值 |
5 |
4 |
2*** |
|
甲採一、乙採二，乙採二、甲採二，甲採二、乙採三，乙採三、甲採一
由上推論可知，此類問題之解似乎是無穩定解。且若一方的策略可預測，則對方將能利用此情報以增加自己的優勢。
11.3 混策對局
無鞍點的問題應以混策 (mixed strategy)求解。每一玩者之策略以一機率分配來表示：
Xi =甲採策略 i 的機率 (i = 1,….,m)
Yj=乙採策略 j 的機率 (j = 1,…. , n)
其中m與n 為二者可用的策略數。
所有X與Y 均為非負數，且Sum of X 與 Sum of Y 均為1。
以機率表示各策略的選擇次數時稱為混策(mixed strategy)，與此相對應的為純策(pure strategy)。純策之發生機率不是0就是1。
混策的期望報酬 = 
混策之對局必須
，其最優解才能穩定。
Minimax theory: 若可採混策，則必有局值 = 
11.4 圖解法
求甲之最優混策：
|
Strategy |
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
甲之第一策略 |
0 |
-2 |
2 |
|
甲之第二策略 |
5 |
4 |
-3 |
|
甲之第三策略 |
2 |
3 |
-4 |
甲之第三純策為甲之第二純策所凌越，前者可刪除。
|
|
|
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
|
|
機率Y1 |
Y2 |
Y3 |
|
甲採一之機率X1 |
甲之第一策略 |
0 |
-2 |
2 |
|
甲採二之機率1- X1 |
甲之第二策略 |
5 |
4 |
-3 |
乙的每一可用純策下之甲方期望報酬為
|
(Y1, Y2, Y3) |
期望報酬 |
|
(1, 0, 0) |
0X1+5(1-X1)=5-5X1 |
|
(0, 1, 0) |
-2X1+4(1-X1)=4-6X1 |
|
(0, 0, 1) |
2X1-3(1-X1)=-3+5X1 |
參見Fig.11.1 (p.481 of Textbook) ，圖中所示的交點有最小的期望報酬，可求得 X1 = 7/11，故 (X1, X2) = (7/11, 4/11)為甲的最優混策。且局值為 –3 + 5 (7/11) = 2/11。
求乙之最優混策：
期望報酬 = Y1 (5-X1) + Y2 (4-6X1) + Y3 (-3+5X1)
已知X1值代入上式，可得10 Y1* + Y2* + Y3* =1
又，已知Y1* + Y2* + Y3* =1，所以知Y1* =0
Y2*
(4-6X1) + Y3*
(-3+5X1) <= 2/11, when 0<=X1 <=1
Y2*
(4-6X1) + Y3*
(-3+5X1) = 2/11,
when X1 =7/11
由於不等式左側為直線，X1=7/11位於0與1之間時該直線有最大值，該直線恆為水平線且
Y2* (4-6X1) + Y3* (-3+5X1) = 2/11, when 0<= X1
<= 1
將X1 =0與1代入上式求出Y2*與Y3*，乙之最優混策 = (Y1, Y2, Y3) = (0, 5/11, 6/11)。
11.4.1 .sup For 2x2 game (補充內容)
|
|
Player 2 |
|
|
Player 1 |
P11 |
P12 |
|
P21 |
P22 |
|
演算法
|
Step 1. |
檢查是否存在鞍點，若有一個或多個，則以前述第二種範例探討，若無鞍點，則到下一步驟。 |
|
Step 2. |
令 X1*=(P22-P21)/(P11+P22-p12-P21), X2*=1- X1* Y1*=(P22-P12)/(P11+P22-p12-P21), Y2*=1- Y1* |
|
Step 3 |
局值 v = X1* Y1* P11 + X1* (1-Y1*)P12 + (1-X1*)Y1*P21 + (1-X1*)(1-Y1*)P22 |
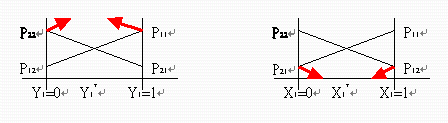
左圖
|
(X1, X2) |
Expected payoff |
|
(1,0) |
P11X1Y1+P12X1Y2= P11Y1+P12(1-Y1) <= v bar ……..(1) |
|
(0,1) |
P21X2Y1+P22X2Y2= P21Y1+P22(1-Y1) <= v bar………(2) |
|
(1)=(2) |
P11Y1*+P12(1-Y1*) = P21Y1*+P12(1- Y1*) , 可求出Y1*=(P22-P12)/(P11+P22-p12-P21) |
右圖
|
(Y1, Y2) |
Expected payoff |
|
(1,0) |
P11X1+P21(1-X1) >= v sub……..(3) |
|
(0,1) |
P12X1+P22(1-X1) >= v sub………(4) |
|
(3)=(4) |
P11X1*+P21(1-X1*) = P12X1*+P22(1- X1*) , 可求出X1*=(P22-P21)/(P11+P22-p12-P21) |
11.5 以LP 求解
考慮甲方
|
Maximize (Xm+1) or minimize (-Xm+1) |
|
|
s.t. |
P11X1 + P21X2 + ….. + Pm1Xm – Xm+1 >=0 P12X1 + P22X2 + ….. + Pm2Xm – Xm+1 >=0 …. P1nX1 + P2nX2 + ….. + PmnXm – Xm+1 >=0 X1 + X2 + ….. + Xm = 1 Xi >=0, I = 1,2,….,m |
|
|
|
考慮乙方
|
Minimize (-Yn+1) |
|
|
s.t. |
P11Y1 + P12Y2 + ….. + P1nYn – Yn+1 <=0 P21Y1 + P22Y2 + ….. + P2nYn – Yn+1 <=0 …. Pm1Y1 + Pm2Y2 + ….. + PmnYn – Yn+1 <=0 Y1 + Y2 + ….. + Yn = 1 Yj >=0, j = 1,2,…,n |
|
|
|
範例
|
|
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
|
機率Y1 |
Y2 |
Y3 |
|
甲採一之機率X1 |
0 |
-2 |
2 |
|
甲採二之機率X2 |
5 |
4 |
-3 |
|
|
取大 |
取大 |
取大 |
|
|
再取小 = v bar = X3 = 上限 |
||
考慮甲方，則乙為(1,0,0), (0,1,0) or (0,0,1)
|
Maximize X3 |
|
|
s.t. |
0 X1 + 5 X2 >= X3 -------à 0 X1 + 5 X2 – X3 >= 0 -2 X1 + 4 X2 >= X3--------à -2 X1 + 4 X2 - X3 >= 0 2 X1 –3 X2 >= X3 --------à 2 X1 –3 X2 - X3 >=0 X1 + X2 = 1 X1, X2, X3 >=0 |
|
|
|
可得出最優原題解：X1*=7/11, X2*=4/11, X3*=2/11
可得出最優偶題解：Y1*=0, Y2*=5/11, Y3*=6/11, Y4*=2/11
考慮乙方，則甲為(1,0) or (0,1)
|
|
乙之第一策略 |
乙之第二策略 |
乙之第三策略 |
|
|
|
|
機率Y1 |
Y2 |
Y3 |
|
|
|
甲採一之機率X1 |
0 |
-2 |
2 |
取小 |
再取大 |
|
甲採二之機率X2 |
5 |
4 |
-3 |
取小 |
|
Minimize Y4 |
|
|
s.t. |
0 Y1 - 2 Y2 + 2Y3 <= Y4-------à 0 Y1 - 2 Y2 + 2Y3 - Y4 <=0 5 Y1 + 4 Y2 - 3Y3 <= Y4--------à5 Y1 + 4 Y2 - 3Y3 - Y4 <=0 Y1 + Y2 + Y3 = 1 Y1, Y2, Y3, Y4 >=0 |
|
|
|
可得出最優原題解：Y1*=0, Y2*=5/11, Y3*=6/11, Y4*=2/11
可得出最優偶題解：X1*=7/11, X2*=4/11, X3*=2/11
11.6 延伸
非零和局 (nonzero-sum game)
競局 (n-person game, n>2)：
非合作局 (Non-cooperative game)
合作局 (Cooperative game)
無窮局 (Infinite game)：玩者有無限多種純策可供選擇