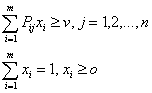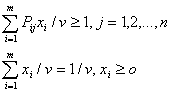11.7 另一種LP 解法
For Player A
|
Max. v s.t. Max. v = Min. (1/v) |
Define Z=1/v, Define X1=x1/v, X2=x2/v, …, Xm=xm/v The problem becomes Min. Z= X1+X2+…+Xm s.t. P11 X1 + P21X2 + ….+ Pm1Xm >=1 P12 X1 + P22X2 + ….+ Pm2Xm >=1 ……… P1nX1 + P2nX2 + ….+ PmnXm >=1 X1+X2+…+Xm=1/v X1, X2, …, Xm >= 0 |
For Player B
|
The problem becomes Max. w = Y1+Y2+…+Yn s.t. P11 Y1 + P12Y2 + ….+ P1nYn <=1 P21 Y1 + P22Y2 + ….+ P2nYn <=1 ……… Pm1Y1 + Pm2Y2 + ….+ PmnYn <=1 Y1+Y2+…+Yn=1/v Y1, Y2, …, Yn >= 0 Where, w=1/v, Yi = yj/v |
範例:
|
|
B之1 |
B之2 |
B之3 |
Row min |
|
A之1 |
3 |
-1 |
-3 |
-3 |
|
A之2 |
-3 |
3 |
-1 |
-3 |
|
A之3 |
-4 |
-3 |
3 |
-4 |
|
Col. Min |
3 |
3 |
3 |
|
下限 (maximin value)為-3, 上限(minimax value)為3,答案可能為負數或0。建議加上任一絕對值大於3的數(K)來轉化上列payoff table. 以加5為例說明:
new payoff table:
|
|
B之1 |
B之2 |
B之3 |
|
A之1 |
8 |
4 |
2 |
|
A之2 |
2 |
8 |
4 |
|
A之3 |
1 |
2 |
8 |
B’s LP model is thus given as
Max. w= Y1+Y2+Y3
s.t.
8Y1+4Y2+2Y3 <=1
2Y1+8Y2+4Y3 <=1
1Y1+2Y2+8Y3 <=1
Y1,Y2,Y3>=0
Final optimum tableau
|
Basic |
Y1 |
Y2 |
Y3 |
S1 |
S2 |
S3 |
Solution |
|
W |
0 |
0 |
0 |
5/49 |
11/196 |
1/14 |
45/196 |
|
Y1 |
1 |
0 |
0 |
1/7 |
-1/14 |
0 |
1/14 |
|
Y2 |
0 |
1 |
0 |
-3/98 |
31/196 |
-1/14 |
11/196 |
|
Y3 |
0 |
0 |
1 |
-1/98 |
-3/98 |
1/7 |
5/49 |
Thus, for the original problem,
v*=1/w-K=196/45-5=-29/45
y1*=Y1/w=(1/14)/(45/196)=14/45
y2*=Y2/w=(11/196)/(45/196)=11/45
y3*=Y3/w=(5/49)/(45/196)=20/45
練習
以Excel 或 LINDO 求解下列問題
|
|
B 之1 |
B 之2 |
|
A之1 |
4 |
-6 |
|
A之2 |
-5 |
8 |
|
A之3 |
3 |
-4 |
求出A與B之混策
11.8 Brown 演算法
|
|
乙 |
|
1) |
2) |
3) |
4) |
5) |
6) |
7) |
8) |
9) |
10) |
|
||||
|
甲 |
1 |
-2 |
3 |
3 |
1 |
4 |
7 |
5 |
3 |
1 |
4 |
7 |
10 |
2/10 |
||||
|
1 |
3 |
-2 |
-2 |
1 |
-1 |
-3 |
0 |
3 |
6 |
4 |
2 |
0 |
0 |
|||||
|
4 |
2 |
1 |
1 |
3 |
4 |
5 |
7 |
9 |
11 |
12 |
13 |
14 |
8/10 |
|||||
|
1) |
1 |
3 |
-2 |
|
假設甲由策略2開始,綠色格為該列之最小, |
|
||||||||||||
|
2) |
2 |
1 |
1 |
|
乙會選策略3,黃色格為該欄之最大,甲改策略1, 累計目前所選之列,綠色格為該列之最小,甲改2, |
|
||||||||||||
|
3) |
6 |
3 |
2 |
|
累計目前所選之欄,黃色格為該欄之最大,甲改3, 累計目前所選之列,乙改3,……. |
|
||||||||||||
|
4) |
10 |
5 |
3 |
|
|
|
||||||||||||
|
5) |
11 |
3 |
6 |
|
|
|
||||||||||||
|
6) |
15 |
5 |
7 |
|
進行10次的運算可知, |
|
||||||||||||
|
7) |
19 |
7 |
8 |
|
下限為 11/10=1.1,上限為 14/10=1.4, |
|
||||||||||||
|
8) |
23 |
9 |
9 |
|
分母為運算的次數,分子為最後之累計值。 |
|
||||||||||||
|
9) |
27 |
11 |
10 |
|
|
|
||||||||||||
|
10) |
31 |
13 |
11 |
|
Y*=[0, 4/10, 6/10], X*=[2/10 0 8/10]T |
|
||||||||||||
|
0 |
4/10 |
6/10 |
|
分母為運算的次數,分子為各列或欄被選中的次數。 |
|||||||||||||
Note:
最終解為 1.33
練習
1 在下列4小題中以Brown 演算法各作五次的反覆計算
|
4 |
2 |
5 |
2 |
|
2 |
4 |
5 |
2 |
|
2 |
3 |
1 |
4 |
|
2 |
1 |
4 |
5 |
|
1 |
6 |
4 |
3 |
|
3 |
2 |
6 |
1 |
|
4 |
3 |
3 |
2 |
2 |
6 |
|
4 |
-3 |
-2 |
|
6 |
0 |
4 |
2 |
6 |
2 |
|
-3 |
4 |
-2 |
|
0 |
7 |
3 |
6 |
2 |
2 |
|
0 |
0 |
1 |
2 同上題撰寫程式各作500次的反覆計算