Chap 10. Dynamic Programming 動態規劃

10.1 典型範例：驛馬車問題The stagecoach problem. 1

10.2 DP問題的特徵 (Characteristics) 21

10.3 確定性動態規劃.. 34

10.3.1 研究DP 問題的自我問卷... 59

10.3.2 如何分辨所面對之確定性 DP 問題... 71

10.3.3 確定性DP 問題範例... 80

10.4 機率性 DP 問題.. 262

微電腦程式 DPPS.exe 使用介紹.. 361

作業 2. 407

動態規劃 (Dynamic Programming, 簡稱 DP)又名多階段規劃(multistage programming)，是在做一系列相關決策(making a sequence of interrelated decisions)時的支援工具，其提供系統化的方法來尋求各個相關的決策，在整合後可得到整體上最佳的效益 (maximizes overall effectiveness)。

補充說明：本章各範例同時使用Excel 求解，請下載相關軟體。

10.1 典型範例：驛馬車問題The stagecoach problem

Fig. 10.1 p.426 of TextBook

名詞說明: 狀態 (state)，階段 (stage)，決策、策略 (policy)

在每一分支皆選擇最小者並不保證可得整體為最小，如上圖可得A-B-F-I-J，total cost 為 13，然而A-D-F 的路徑卻優於A-B-F。

驛馬車問題(StageCoach problem)可視為最短路徑問題(Shortest-Route problem)的特例，此時各分枝上的值可視為成本而非距離。StageCoach 問題可用解 Shortest-Route 問題的方法求出答案，亦可用 DP 的方法求解。

驛馬車問題與最短路徑問題有些根本上的差別。

後者允許逆流。

後者的各node 之間不易明顯的區分出各個階段 (STAGE)。

前者在同一階段間的各狀態(node)間沒有連線。

模式建立Formulation:

f_n^*(s) = MIN f_n(s,X_n)=f_n(s,X_n^*)

其中，f_n(s, X_n) 為在階段n的狀態點s，依照既定策略在後續的所有階段中有一最佳成效的現階段總成本。(The total cost of the best overall policy for the remaining stages when in state s, ready to start stage n.)

fn(s,X_n) = immediate cost (stage n) + minimum future cost

= C_sXn + f_n+1^*(Xn) = 本階段立即的成本 + 後續階段的最低總成本

驛馬車問題DP 解法

求解步驟:

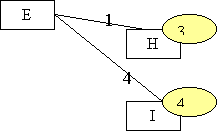
n=4, State J is reached at the end of stage 4, thus, f₅^*(J)=0

s	CsXn + f5^*(J)	f4^*(s) = min [CsXn + f5^*(J)]
	J	f4^*(s)	X4^*
H	3	3	J
I	4	4	J

n=3

s		f3=C+f4^*				f3^*(s)		X3^* n=3時在下一階段的最佳目標狀態點
		H		I
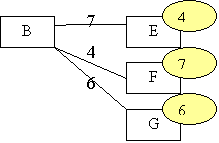
	E		4		8		4	H
	F		9		7		7	I
	G		6		7		6	H

s	H	I
E	1	4
F	6	3
G	3	3

n=2

	f2=C+f3^*			f2^*(s)	X2^*
s	E	F	G
B	11	11	12	11	E, F
C	7	9	10	7	E
D	8	8	11	8	E, F

s	E	F	G
B	7	4	6
C	3	2	4
D	4	1	5

n=1

	f1=C+f2^*			F1^*(s)	X1^*
s	B	C	D
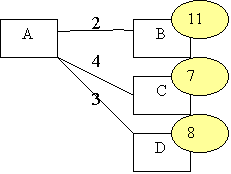
A	13	11	11	11	C, D

s	B	C	D
A	2	4	3

Solution:

A – D –F –I – J

A – D –E –H – J

A – C –E –H – J

10.2 DP問題的特徵 (Characteristics)

任何與驛馬車問題有類似結構者皆可用動態規劃的方法求解。此類問題的特徵包括：

1. 此問題可依階段分類，各階段可用策略來決定下一步。

2. 各階段包括數個狀態點 (狀態點的數量沒有限制，可以是有限個也可以無限個)。

3. 在各個階段所涉及的策略旨在將目前的狀態點由所在的階段轉化至下一階段的另一狀態點 (依據機率分布來轉化亦是可行)。

4. 求解步驟的設計是用來找出針對整個問題的最佳策略。

5. 就任一狀態點而言，後續階段的最佳策略與前面階段之最佳策略無關。

6. 求解步驟由尋求前一階段的每一個狀態點的最佳策略開始。

7. 對階段n的每一狀態點建立一遞迴的關係式，此式也適用於階段n+1的每一狀態點。

8. 透過此遞迴關係式，求解步驟由最末階段一階段一階段的回溯，尋求各階段的最佳對策，直到抵達最初階段。

10.3 確定性動態規劃

由上節所述的特徵2與3，可將DP模式分類為以下所述的三種型態：分別為確定性動態規劃模式、機率性動態規劃模式、馬可夫決策分析模式。

確定性動態規劃模式- Deterministic DP
	完全由現階段的狀態點與策略來決定最佳對策是朝向下一階段的哪一個狀態點前進。各階段中狀態點的個數不限制，各階段可以有離散的有限個或連續的無限個狀態點。
非確定（機率）性動態規劃模式- Probabilistic DP
	各階段存在有限數量個狀態點的機率性動態規劃模式，透過機率分布來決定下一個狀態點。
馬可夫決策分析模式- Markovian Analysis
	各階段存在無限多個狀態點的機率性動態規劃模式。

以下所列為典型的 DP 問題，可透過DP模式的解法求解：

1. 市場策略	Marketing Strategy
2. 工作排程	Job Shop Scheduling
3. 人力分配	Work Force Assignment
4. 生產及庫存安排	Production & Inventory Scheduling
5. 庫存控制	Inventory Control
6. 計劃管理	Project Management
7. 汰舊換新	Replacement
8. 路線安排	Grand Tour Scheduling
9. 資金預算	Capital Budgeting
10. 載貨分配	Cargo Loading
11. 可靠度分析	Reliability

10.3.1 研究DP 問題的自我問卷

當你透過DP問題特徵的辨識，了解到所面對的問題就是標準的DP問題時，下一步就是要問自己以下的幾個問題，以協助建立DP模式。

1. 策略或稱決策變數為何？ What are the policy or decision variable?

2. 最佳策略的目標函數為何？What is the criterion or objective function for determining an optimal policy?

3. 此問題的特徵為何？依階段進行分析。How is the problem characterized and then analyzed in terms of stages?

4. 各階段中狀態點的特徵為何？What characterizes the state of the problem at each stage?

5. 各項限制如何影響各狀態點與決策變數的可行解？How does the constraints influence the states of the problem and the feasible values of the policy variables?

一旦此問題中某一階段的模式建立完成且可引申適用於多階段，我們可算是完成初步的工作，可朝向進一步分析此DP問題的動態行為邁進。

10.3.2 如何分辨所面對之確定性 DP 問題

如何分辨所面對之確定性 DP 問題？ 可由目標函數或由各階段中的狀態著手。

由目標函數的形式 (form) 著手

最小化來自各階段的貢獻值的總和(minimize the sum of the contribution from the individual stages)，此類型屬於與驛馬車問題同類。

同上類型但目標函數為求最大化。此類型屬於與載貨(Cargo loading)問題同類。

最小化來自各階段的貢獻值的積 (minimize a product of such terms)，此類型屬於與可靠度(Reliability)問題同類。

由各階段中各狀態點的天性 (Nature) 著手

各階段中的狀態可以是離散的，如驛馬車問題所示。

各階段中的狀態可以是連續的，如教科書中example 4 (p.444)所示的勞動力規劃(Scheduling Employment Levels)問題所示。

各階段中的狀態可以由狀態向量表示，此時包括多個變數，如教科書中example 5 (p.450)所示。

10.3.3 確定性DP 問題範例

Example 2: Distributing Medical Teams to Countries (p.434 of Text Book)

屬成效分配問題 (Distribution of Effort)

醫療隊伍數量	增加的1000 人年的生命
	國家1	國家2	國家3
0	0	0	0
1	45	20	50
2	70	45	70
3	90	75	80
4	105	110	100
5	120	150	130

Maximize

Subject to

其中， Xi 為非負整數，5為總資源數量

Transformation

定義 , 階段n時可分配至 第n,...3個國家之醫療隊伍數目

Stage	n	Xn	n+1
State	sn	----------------à	sn-xn
Value	fn(sn,xn)	pn(xn)	fn+1^*(sn-xn)

Solution Procedure:

n=3: s₃=5-x₁-x₂ = 在第 3階段時仍剩餘之隊伍數

s3	f3^*(s3)	x3^*
0	0	0
1	50	1
2	70	2
3	80	3
4	100	4
5	130	5

n=2: s₂=5-x₁ =在第 2階段時仍剩餘之隊伍數

s2	f2 = p2(x2) + f3^*(s2-x2) x2 = 留在國家2之隊伍數						f2^*(s2)	x2^*
	0	1	2	3	4	5
0	0						0	0
1	50	20					50	0
2	70	70	45				70	0 or 1
3	80	90	95	75			95	2
4	100	100	115	125	110		125	3
5	130	120	125	145	160	150	160	4

n=1: s₁=5

s1	f1 = p1(x1) + f2^*(s1-x1) x1 = 留在本國之隊伍數						f1^*(s1)	x1^*
	0	1	2	3	4	5
5	160	170	165	160	155	120	170	1

Solution: x₁^* = 1, thus, s₂=4, thus, x₂^* = 3, thus, s₃=1, thus, x₃^* = 1

圖解法：請參見下載的Excel 檔案

Example 3: Distributing Scientists to Research Teams

本題亦屬「成效分配」（Distribution of Effort） 問題。

某工程計畫遭遇困難，各組失敗之機率初步估計分別為0.4, 0.6, 0.8，假設各組增加一至二個科學家後，其失敗之機率如下表，應如何分配此二新科學家使失敗之機率為最小?

新科學家 人數	失 敗 的 機 率
	小 組 1	小 組 2	小 組 3
0	0.4	0.6	0.8
1	0.2	0.4	0.5
2	0.15	0.2	0.3

Minimize

s.t.

其中， x_i為非負整數

Where,

Solution Procedure:

n=3

s3	f3^*(s3)	x3^*
0	0.8	0
1	0.5	1
2	0.3	2

n=2

s2	f2=p2(x2)+f3^*(s2-x2)			f2^*(s2)	x2^*
	0	1	2
0	0.6*0.8=0.48			0.48	0
1	0.6*0.5=0.3	0.4*0.8=0.32		0.30	0
2	0.6*0.3=0.18	0.4*0.5=0.2	0.2*0.8=0.16	0.16	2

n=1

s1	f1=p1(x1)+f2^*(s1-x1)			f1^*(s1)	x1^*
	0	1	2
2	0.4*0.16=0.064	0.2*0.3=0.06	0.15*0.48=0.072	0.06	1

Solution: x₁^*=1, s₂=2-1=1, x₂^*=0, s₃=1-0=1, x₃^*=1,

圖解法：

Example 4: Scheduling Employment Levels (p.444)

員工聘雇人數問題：

以下各季至少需維持之人數(R_n)如下：

春	夏	秋	冬	春
255	220	240	200	255
Stage	1	2	3	4

任何超過此人數(R_n)之聘雇皆需多花費 $ 2000/人/季，

各季之聘雇人數若有變動，則皆需要多花費 $200*(變動人數)²，

聘雇人數允許含小數點之數目，因為有時會聘雇臨時工人。

建立模式：

假設X_n為各季實際聘雇之人數(employment level for stage n)

且R_n ≦ X_n ≦ 255 (各個 Stage 有無限多個 State)

Cost for Stage n = 200 (x_n-x_n-1)² + 2000 (x_n-R_n)

State s_n = x_n-1, when n=1, s₁=x₀=x₄=255

選取x₁,x₂,x₃ 使得

Minimize

Subject to

n=4, 為末項為0, 同時

所以，

遞迴關係式：

由上式，可依序求出

n=4	s4	f4^*(s4)	x4^*
	200<=s4<=255	200(255-s4)^2	255
n=3	s3	f3^*(s3)	x3^*
	240<=s3<=255	50(250-s3)^2+50(260-s3)^2+1000(s3-150)	(s3+250)/2
n=2	s2	f2^*(s2)	x2^*
	220<=s2<=240	200(240-s2)^2+115000	240
	240<=s2<=255	(200/9)[(240-s2)^2+(255-s2)^2+(270-s2)^2]+2000(s2-195)	(2s2+240)/3
n=1	s1	f1^*(s1)	x1^*
	255	185000	247.5

Example 5: Wyndor Glass Company Problem (p.450)

LP 問題 以 DP 來求解

Maximize	Z = 3X1 + 5 X2
s.t.	X1 <=4
	2X2 <=12
	3X1+2X2 <=18
	X1>=0, X2>=0

另例：Cargo Loading Problem 卸貨問題

Consider loading a vessel with stocks of n items. Each unit of

item has a weight of Wi and a value of Vi （i = 1, 2,.. n)

The maximum cargo weight is W. Find number of units to load for

each item in order to maximize the value of the cargo.

maximize SVi Ki, for i = 1 to n

s.t. SWi Ki ≦ W, for i = 1 to n

其中 Ki 為非負整數

i	Wi	Vi
1	2	65
2	3	80
3	1	30

Solution Procedures:

Stage 3: V₃ K₃ =30 K₃

	K3 =0	1	2	3	4	[5/1]
	V3 K3=0	30	60	90	120	150	f3(Y3) =Max(V3 K3)	K3^*
Y3=0	0	-	-	-	-	-	0	0
Y3=1	0	30	-	-	-	-	30	1**
Y3=2	0	30	60	-	-	-	60	2
Y3=3	0	30	60	90	-	-	90	3
Y3=4	0	30	60	90	120	-	120	4
Y3=5	0	30	60	90	120	150	150	5

Stage 2: V₂ K₂ = 80 K₂+f₃(Y₂–3 K₂)

	K2 = 0	K2 =[5/3]=1
	V2 K2 =0	V2 K2 =80	f2(Y2) =Max(V2 K2)	K2^*
Y2 = 0	0+ 0= 0	-	0	0
1	0+ 30= 30	-	30	0 **
2	0+ 60= 60	-	60	0
3	0+ 90= 90	80 + 0=80	90	0
4	0+120=120	80+30=110	120	0
5	0+150=150	80+60=140	150	0

Stage 1: V₁ K₁=65 K₁+f₂(Y₁-2 K₁)

	K1 = 0	K1 = 1	K1 = [5/2]=2
	V1 K1 =0	V1 K1=65	V1 K1=130	f1(Y1) = Max (V1 K1)	K1^*
Y1 = 0	0+ 0= 0	-	-	0	0
1	0+30=30	-	-	30	0
2	0+60=60	65+ 0=65	-	65	1
3	0+ 90= 90	65+ 30= 95	-	95	1
4	0+120=120	65+ 60=125	130+0=130	130	2
5	0+150=150	65+ 90=155	130+30=160	160	2**

Optimum Solution ： K₁^* ， K₂^* ， K₃^* = 2, 0, 1, with a total value of 160

二、圖解法：略

10.4 機率性 DP 問題

Probabilistic DP Problem

Suppose that the objective is to minimize the expected sum of the contributions from the individual stages.

f_n(s_n,x_n) would represent the minimum expected sum from stage n onward, given that the state and policy decision at stage n are s_n and x_n, respectively.

s_n: 階段 n 之某一狀態點

x_n: 階段 n 某一狀態點使用之 policy decision.

C_i: 階段 n 對目標函數之貢獻

the contribution of stage n to the objective function.

s : 階段 n+1 中狀態點之數目

the number of possible states at stage n+1.

Consequently,

with

Example 6: Determining Reject Allowances p.454

某公司接受一訂單製造某特種產品一件，訂購人對產品之品質要求很高，公司估計每件製造出的產品，其可能合格之機率為1/2。由於時間有限，只能允許三次製程（PRODUCTION RUN），請問每次製程應製造幾件產品，使總製造成本為最小? 其中涉及成本之項目如下：

每件產品材料費 100 元，每次製程重 RUN 皆須 300 元的設置成本，若經過三次製程後仍無一產品合格，則不僅沒有收入，且會被罰款，共損失 1600 元。

解：三次製程視為三個階段，階段 n 的狀態與決策分別為 Sn 與 Xn

Sn: 在階段 n 仍缺佳品的個數， 0 or 1

Xn: 在階段 n 所製造之產品數目

fn(Sn, Xn) 為 階段 n 至 3 的 總期望成本

f_n^*(s_n) = MIN {f_n(s_n,x_n)} for x_n= 0,1..

假設以 100 元為單位，階段 n 涉及之成本為 K + x_n, 其中K=0 if x_n= 0, K=3 if x_n > 0

f_n+1^*(1)：至第 n+1 階段仍差一個成品，表示前階段之x_n 個全部失敗，

f₄^*(1) = 16

For Sn=1:

f_n(1, Xn) = K + Xn + (1/2)^Xn * f_n+1^*(1)+ (1-(1/2)^Xn)* f_n+1^* (0)

The recursive relationship

f_n^*(1) = MIN {K + Xn + (1/2)^Xn * f_n+1^*(1)} for Xn=0,1,.

Value:

f_n(1,x_n) = K + x_n + (1/2)^Xn * f_n+1^*(1)

n=3：f₃(1, X₃)= K + X₃ + 16*(1/2)^X3

s	x=0	1	2	3	4	5	f^*(s)		X^*
3	3						3	3	3
0	0							0	0
1	16	12	9	8	8	8+(1/2)		8	3 or 4

n=2：f₂(1, x₂)= K + x₂ + (1/2)^X2 f₃^*(1)

s	x=0	1	2	3	4	f^*(s)		x^*
2	2					2	2	2
0	0						0	0
1	8	8	7	7	7+(1/2)		7	2 or 3

n=1：f₁(1, x₁)= K + x₁ + (1/2)^X1 f₂^*(1)

s	x=0	1	2	3	4	f^*(s)		x^*
1	1					1	1	1
		1	3	7	7	3
1	7	7-	6-	6-	7--	6---		2
		2	4	8	16	4

Example 7 Winning in Las Vegas (p456)

年輕的統計學家相信自己有一個好方法可在賭城贏錢，其每一盤都有2/3的勝算。其同事不相信，於是兩人打賭，打賭的條件是以三個籌碼開始，在三盤之後，年輕的統計學家不會剩餘有至少五個籌碼。每盤可下注手上有的任意數量的籌碼，贏時可獲得等量的籌碼。請以DP來決定此三盤該如何下注才能有最大的勝算以贏得與同事的賭注。

Stage n =局數. x_n =第n局下注的籌碼數. State s_n =第n局下注前手上的籌碼數.

n=3,

s3	x3=0	1	2	3	4	5	f3^*(s3)	x3^*
0	0						0
1	0	0					0
2	0	0	0				0
3	0	0	2/3	2/3			2/3	2(or more)
4	0	2/3	2/3	2/3	2/3		2/3	1(or more)
>=5	1	2/3	2/3	2/3	2/3	2/3	1	0(or <s3-5)

n=2,

s2	X2=0	1	2	3	4	f2^*(s2)	x2^*
0	0					0
1	0	0				0
2	0	4/9	4/9			4/9	1 or 2
3	2/3	4/9	2/3	2/3		2/3	0,2,or 3
4	2/3	8/9	2/3	2/3	2/3	8/9	1
>=5	1					1	0(or <s2-5)

n=1,

S1	x1=0	1	2	3	f1^*(s1)	x1^*
3	2/3	20/27	2/3	2/3	20/27	1

計算過程請參見Excel 檔案之例七

微電腦程式 DPPS.exe 使用介紹

範例一、輸入資料檔格式: 檔名 CPM1.DAT 之內容如下：

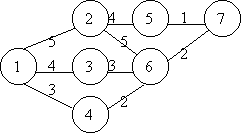
程式計算結果如下：

StageCoach problem with 4 stages

------------------------------------------------------------------

# of NODEs = 1 2 3 4 5 6 7 8 9

Stage 1 : 1

Stage 2 : 2 3 4

Stage 3 : 5 6

Stage 4 : 7

------------------------------------------------------------------

# of Branches = 1 2 3 4 5 6 7 8

C(1, 1, K) = 5.00 4.00 3.00

C(2, 1, K) = 4.00 5.00

C(2, 2, K) = 3.00

C(2, 3, K) = 2.00

C(3, 1, K) = 1.00

C(3, 2, K) = 2.00

------------------------------------------------------------------

THE OPTIMUM ROUTE IS : 1 4 6 7

THE MINIMUM COST IS : 7

範例二、輸入資料檔格式: 檔名 CPM2.DAT

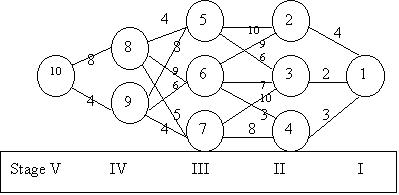
程式計算結果如下：

StageCoach problem with 5 stages

------------------------------------------------------------

# of NODEs = 1 2 3 4 5 6 7 8 9

Stage 1 : 1

Stage 2 : 2 3 4

Stage 3 : 5 6 7

Stage 4 : 8 9

Stage 5 : 10

------------------------------------------------------------

# of Branches = 1 2 3 4 5 6 7 8

C(1, 1, K) = 4.00 2.00 3.00

C(2, 1, K) = 10.00 9.00

C(2, 2, K) = 6.00 7.00 10.00

C(2, 3, K) = 3.00 8.00

C(3, 1, K) = 4.00 8.00

C(3, 2, K) = 9.00 6.00

C(3, 3, K) = 5.00 4.00

C(4, 1, K) = 8.00

C(4, 2, K) = 4.00

------------------------------------------------------------

THE OPTIMUM ROUTE IS : 1 4 6 9 10

THE MINIMUM COST IS : 16

作業 2

1. 本章作業10.3.1

2. 本章作業10.3.10

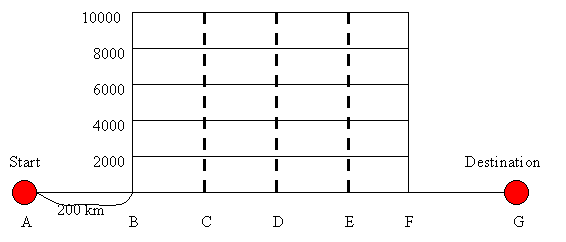
3. 某航空班次由甲地 (A)飛往乙地 (G)，兩地相距1200公里。如圖所示甲地(A)至乙地(G)之間(含A,G)共七個管制點各相距200公里，請規劃航線(找出在B至F點上空的飛航高度) 使飛機的耗油量為最少。如表所示為每飛航200 公里地面距離依據爬昇或下降高度的耗油量(kg)。 (請利用 DPPS.EXE 求解，輸入資料檔名規定為: HW2-3.DAT, 計算結果存於: HW2-3.RLT)

4. 同上題，請以圖解法求解。

表1: 每200 公里地面距離的耗油量(kg)

開始高度，m	飛抵高度，m
	0	2000	4000	6000	8000	10000
0	-	1500	1800	2070	2300	2500
2000	300	600	1000	1500	1950	2300
4000	120	180	300	840	1160	1730
6000	0	60	120	200	600	1200
8000	0	0	30	80	180	600
10000	0	0	0	0	60	90

5. OR-Chap10 中的Sup-1 工作表中所列的作業

6. OR-Chap10 中的Sup-2 工作表中所列的作業

7. OR-Chap10 中的Sup-3 工作表中所列的作業